| Chapitre 1 |
 Résumé des notes de cours chap1 Résumé des notes de cours chap1 |
|
|
 Vidéo de théorie et exercices -Opérations sur les polynômes Vidéo de théorie et exercices -Opérations sur les polynômes |
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
 Vidéo de théorie et exercices-Mise en évidence Vidéo de théorie et exercices-Mise en évidence |
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
 Vidéo de théorie et exercices-Identités du second degré Vidéo de théorie et exercices-Identités du second degré |
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
 Vidéo de théorie et exercices-Factorisation du second degré Vidéo de théorie et exercices-Factorisation du second degré |
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
 Corrigé avec démarche complétion de carré a à e Corrigé avec démarche complétion de carré a à e |
Corrigé avec démarche complétion de carré a à e |
|
 Corrigé avec démarche complétion de carré f à i Corrigé avec démarche complétion de carré f à i |
Corrigé avec démarche complétion de carré f à i |
|
 Corrigé avec démarche complétion de carré j à l Corrigé avec démarche complétion de carré j à l |
Corrigé avec démarche complétion de carré j à l |
|
 Vidéo de théorie et exercices-Fractions algébriques Vidéo de théorie et exercices-Fractions algébriques |
|
|
1- Écouter la vidéo ci-dessous.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
Attention!
Petite coquille dans la vidéo, à l'exemple E.
On devrait lire a²+5a+ 6 et non a²+5x+ 6.
|
|
|
|
 Vidéo de théorie et exercices-Addition et soustraction de fractions algébriques Vidéo de théorie et exercices-Addition et soustraction de fractions algébriques |
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Vidéo de théorie et exercices-Multiplication et division de fractions algébriques Vidéo de théorie et exercices-Multiplication et division de fractions algébriques |
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Exercices de révision du chapitre 1 Exercices de révision du chapitre 1 |
Exercices de révision du chapitre 1 |
|
| Chapitre 2 |
 Résumé des notes de cours chapitre 2 Résumé des notes de cours chapitre 2 |
Résumé des notes de cours chapitre 2 |
|
 Vidéo de théorie et exercices-Les fonctions et leurs propriétés Vidéo de théorie et exercices-Les fonctions et leurs propriétés |
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Vidéo de théorie et exercices-Fonction en escalier Vidéo de théorie et exercices-Fonction en escalier |
|
1- Écouter la vidéo ci-dessous.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Vidéo de théorie et exercices-Fonction polynominale de degré 2 (quadratique) Vidéo de théorie et exercices-Fonction polynominale de degré 2 (quadratique) |
|
1- Écouter la vidéo ci-contre.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Vidéo de théorie et exercices-Fonction exponentielle Vidéo de théorie et exercices-Fonction exponentielle |
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Changement de base Changement de base |
Loi sur le changement de base :
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'math17f39f8317fbdb1988ef4c628eb'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAADRjdnQgDVUNBwAAAVAAAAA6Z2x5ZoPi2VsAAAGMAAAAsmhlYWQQC2qxAAACQAAAADZoaGVhCGsXSAAAAngAAAAkaG10eE2rRkcAAAKcAAAACGxvY2EAHTwYAAACpAAAAAxtYXhwBT0FPgAAArAAAAAgbmFtZaBxlY4AAALQAAABn3Bvc3QB9wD6AAAEcAAAACBwcmVwa1uragAABJAAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACAAAAAEAAQAAQAAAD3%2F%2FwAAAD3%2F%2F%2F%2FEAAEAAAAAAAABVAMsAIABAABWACoCWAIeAQ4BLAIsAFoBgAKAAKAA1ACAAAAAAAAAACsAVQCAAKsA1QEAASsABwAAAAIAVQAAAwADqwADAAcAADMRIRElIREhVQKr%2FasCAP4AA6v8VVUDAAACAIAA6wLVAhUAAwAHAGUYAbAIELAG1LAGELAF1LAIELAB1LABELAA1LAGELAHPLAFELAEPLABELACPLAAELADPACwCBCwBtSwBhCwB9SwBxCwAdSwARCwAtSwBhCwBTywBxCwBDywARCwADywAhCwAzwxMBMhNSEdASE1gAJV%2FasCVQHAVdVVVQAAAAEAAAABAADVeM5BXw889QADBAD%2F%2F%2F%2F%2F1joTc%2F%2F%2F%2F%2F%2FWOhNzAAD%2FIASAA6sAAAAKAAIAAQAAAAAAAQAAA%2Bj%2FagAAF3AAAP%2B2BIAAAQAAAAAAAAAAAAAAAAAAAAIDUgBVA1YAgAAAAAAAAAAoAAAAsgABAAAAAgBeAAUAAAAAAAIAgAQAAAAAAAQAAN4AAAAAAAAAFQECAAAAAAAAAAEAEgAAAAAAAAAAAAIADgASAAAAAAAAAAMAMAAgAAAAAAAAAAQAEgBQAAAAAAAAAAUAFgBiAAAAAAAAAAYACQB4AAAAAAAAAAgAHACBAAEAAAAAAAEAEgAAAAEAAAAAAAIADgASAAEAAAAAAAMAMAAgAAEAAAAAAAQAEgBQAAEAAAAAAAUAFgBiAAEAAAAAAAYACQB4AAEAAAAAAAgAHACBAAMAAQQJAAEAEgAAAAMAAQQJAAIADgASAAMAAQQJAAMAMAAgAAMAAQQJAAQAEgBQAAMAAQQJAAUAFgBiAAMAAQQJAAYACQB4AAMAAQQJAAgAHACBAE0AYQB0AGgAIABGAG8AbgB0AFIAZQBnAHUAbABhAHIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlACAATQBhAHQAaAAgAEYAbwBuAHQATQBhAHQAaAAgAEYAbwBuAHQAVgBlAHIAcwBpAG8AbgAgADEALgAwTWF0aF9Gb250AE0AYQB0AGgAcwAgAEYAbwByACAATQBvAHIAZQAAAwAAAAAAAAH0APoAAAAAAAAAAAAAAAAAAAAAAAAAALkHEQAAjYUYALIAAAAVFBOxAAE%2F)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%2217.5%22%20y%3D%2249%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22ae2ef524fbf3d9fe611d5a8e90fefdc%22%20font-size%3D%2219%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2240.5%22%20y%3D%2256%22%3Ea%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2259.5%22%20y%3D%2249%22%3Ec%3C%2Ftext%3E%3Ctext%20font-family%3D%22math17f39f8317fbdb1988ef4c628eb%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%2282.5%22%20y%3D%2249%22%3E%3D%3C%2Ftext%3E%3Cline%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%2299.5%22%20x2%3D%22182.5%22%20y1%3D%2239.5%22%20y2%3D%2239.5%22%2F%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22120.5%22%20y%3D%2224%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2219%22%20text-anchor%3D%22middle%22%20x%3D%22148.5%22%20y%3D%2232%22%3E10%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22171.5%22%20y%3D%2224%22%3Ec%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22119.5%22%20y%3D%2266%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2219%22%20text-anchor%3D%22middle%22%20x%3D%22147.5%22%20y%3D%2274%22%3E10%3C%2Ftext%3E%3Ctext%20font-family%3D%22ae2ef524fbf3d9fe611d5a8e90fefdc%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22171.5%22%20y%3D%2266%22%3Ea%3C%2Ftext%3E%3C%2Fsvg%3E)
Cette loi nous permet, par exemple, de calculer la valeur d'une variable dans une équation exponentielle qui n'utilise pas la base 10.
Exemple : Calcule la valeur de x dans format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%224.5%22%20y%3D%2218%22%3E5%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2212.5%22%20y%3D%2211%22%3Ex%3C%2Ftext%3E%3Ctext%20font-family%3D%22math17f39f8317fbdb1988ef4c628eb%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2224.5%22%20y%3D%2218%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2246.5%22%20y%3D%2218%22%3E202%3C%2Ftext%3E%3C%2Fsvg%3E) . .
On sait que format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%225.5%22%20y%3D%2222%22%3E5%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2215%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2215.5%22%20y%3D%2214%22%3Ex%3C%2Ftext%3E%3Ctext%20font-family%3D%22math17f39f8317fbdb1988ef4c628eb%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%2230.5%22%20y%3D%2222%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%2257.5%22%20y%3D%2222%22%3E202%3C%2Ftext%3E%3C%2Fsvg%3E) correspond à correspond à format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%2213.5%22%20y%3D%2220%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2215%22%20text-anchor%3D%22middle%22%20x%3D%2231.5%22%20y%3D%2226%22%3E5%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%2251.5%22%20y%3D%2220%22%3E202%3C%2Ftext%3E%3Ctext%20font-family%3D%22math17f39f8317fbdb1988ef4c628eb%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%2278.5%22%20y%3D%2220%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2294.5%22%20y%3D%2220%22%3Ex%3C%2Ftext%3E%3C%2Fsvg%3E) . .
Grâce à la l'égalité suivante :
%3C%2Fmo%3E%3Cmi%20mathsize%3D%2226px%22%3En%3C%2Fmi%3E%3C%2Fmsup%3E%3Cmo%20mathsize%3D%2226px%22%3E%26%23x21D4%3B%3C%2Fmo%3E%3Cmi%20mathsize%3D%2226px%22%3En%3C%2Fmi%3E%3Cmo%20mathsize%3D%2226px%22%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmo%20mathsize%3D%2226px%22%3E%3D%3C%2Fmo%3E%3Cmsub%3E%3Cmi%20mathsize%3D%2226px%22%3Elog%3C%2Fmi%3E%3Cmrow%3E%3Cmo%20mathsize%3D%2226px%22%3E(%3C%2Fmo%3E%3Cmi%20mathsize%3D%2226px%22%3Eb%3C%2Fmi%3E%3Cmi%20mathsize%3D%2226px%22%3Ea%3C%2Fmi%3E%3Cmi%20mathsize%3D%2226px%22%3Es%3C%2Fmi%3E%3Cmi%20mathsize%3D%2226px%22%3Ee%3C%2Fmi%3E%3Cmo%20mathsize%3D%2226px%22%3E)%3C%2Fmo%3E%3C%2Fmrow%3E%3C%2Fmsub%3E%3Cmi%20mathsize%3D%2226px%22%3Em%3C%2Fmi%3E%3C%2Fmath%3E--%3E%3Cdefs%3E%3Cstyle%20type%3D%22text%2Fcss%22%3E%40font-face%7Bfont-family%3A'ae2ef524fbf3d9fe611d5a8e90fefdc'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMjv%2FLJYAAADMAAAATmNtYXDgWxEdAAABHAAAADRjdnQgAAAABwAAAVAAAAAEZ2x5ZoYrxVAAAAFUAAAA0WhlYWQOdyayAAACKAAAADZoaGVhC0UVwQAAAmAAAAAkaG10eCg8AIUAAAKEAAAACGxvY2EAAAVKAAACjAAAAAxtYXhwBIoEWwAAApgAAAAgbmFtZXSF9ZsAAAK4AAABrXBvc3QDogHPAAAEaAAAACBwcmVwukanGAAABIgAAAANAAAGtAGQAAUAAAgACAAAAAAACAAIAAAAAAAAAQIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg8AMGe%2F57AAAHPgGyAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACAAAAAEAAQAAQAAAGH%2F%2FwAAAGH%2F%2F%2F%2BgAAEAAAAAAAAABwACAFUAAAMAA6sAAwAHAAAzESERJSERIVUCq%2F2rAgD%2BAAOr%2FFVVAwAAAwAt%2F3QEAwRZAAsAFwAdADsYAbAdELAD1LADELAU1LAUELAc1LAcELAJ1LAcELAOPLAJELAbPACwBhCwEdSwBhCwANSwABCwF9QwMQEiABEWEjMyEjcQJgYWAwIGIyImNTQ2MwE1BhMjEgIBs%2F7fFvWy07oDhYZwFgxOhVmysoUB7YwEslEEWf7f%2Ft71%2Ft8BM%2BMBp5yyLf6d%2FwBlyJzfsvxZjF0B5%2F1eAAAAAAEAAAABAACav9usXw889QADCAD%2F%2F%2F%2F%2F1a3uPf%2F%2F%2F%2F%2FVre49AAH%2B9QQDBkMAAAAKAAIAAQAAAAAAAQAABz7%2BTgAAF3AAAf%2F8BAMAAQAAAAAAAAAAAAAAAAAAAAIDUgBVBEwALQAAAAAAAAAoAAAA0QABAAAAAgAeAAMAAAAAAAIAgAQAAAAAAAQAADsAAAAAAAAAFQECAAAAAAAAAAEAFgAAAAAAAAAAAAIADgAWAAAAAAAAAAMANAAkAAAAAAAAAAQAFgBYAAAAAAAAAAUAFgBuAAAAAAAAAAYACwCEAAAAAAAAAAgAHACPAAEAAAAAAAEAFgAAAAEAAAAAAAIADgAWAAEAAAAAAAMANAAkAAEAAAAAAAQAFgBYAAEAAAAAAAUAFgBuAAEAAAAAAAYACwCEAAEAAAAAAAgAHACPAAMAAQQJAAEAFgAAAAMAAQQJAAIADgAWAAMAAQQJAAMANAAkAAMAAQQJAAQAFgBYAAMAAQQJAAUAFgBuAAMAAQQJAAYACwCEAAMAAQQJAAgAHACPAE0AYQB0AGgAIABGAG8AbgB0ACAAMgBSAGUAZwB1AGwAYQByAE0AYQB0AGgAcwAgAEYAbwByACAATQBvAHIAZQAgAE0AYQB0AGgAIABGAG8AbgB0ACAAMgBNAGEAdABoACAARgBvAG4AdAAgADIAVgBlAHIAcwBpAG8AbgAgADEALgAwTWF0aF9Gb250XzIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlAAAAAAMAAAAAAAADnwHPAAAAAAAAAAAAAAAAAAAAAAAAAAC5ByIAAI2FGACyAAAAAAAA)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'math1d8b8eed422c106ae9d7c55579f'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAADxjdnQgDVUNBwAAAVgAAAA6Z2x5ZoPi2VsAAAGUAAABimhlYWQQC2qxAAADIAAAADZoaGVhCGsXSAAAA1gAAAAkaG10eE2rRkcAAAN8AAAADGxvY2EAHTwYAAADiAAAABBtYXhwBT0FPgAAA5gAAAAgbmFtZaBxlY4AAAO4AAABn3Bvc3QB9wD6AAAFWAAAACBwcmVwa1uragAABXgAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACAD0h1P%2F%2FAAAAPSHU%2F%2F%2F%2FxN4uAAEAAAAAAAAAAAFUAywAgAEAAFYAKgJYAh4BDgEsAiwAWgGAAoAAoADUAIAAAAAAAAAAKwBVAIAAqwDVAQABKwAHAAAAAgBVAAADAAOrAAMABwAAMxEhESUhESFVAqv9qwIA%2FgADq%2FxVVQMAAAIAgADrAtUCFQADAAcAZRgBsAgQsAbUsAYQsAXUsAgQsAHUsAEQsADUsAYQsAc8sAUQsAQ8sAEQsAI8sAAQsAM8ALAIELAG1LAGELAH1LAHELAB1LABELAC1LAGELAFPLAHELAEPLABELAAPLACELADPDEwEyE1IR0BITWAAlX9qwJVAcBV1VVVAAIAgQCBBIACgQAJAA8AjxgBsBAQsAXUsAUQsA%2FUsBEQsADUsAAQsAzUsA4QsAo8sAcQsAM8sAYQsAQ8sAkQsAE8sAgQsAI8sA0QsAs8ALAQELAE1LAEELAD1LADELAK1LAKELAO1LAOELAH1LAHELAG1LAEELABPLADELACPLAKELALPLAPELAMPLAOELANPLAHELAIPLAGELAJPDAxAQU3IRcJAQchJwEhNychBwSA%2FtUr%2FgAr%2FtYBKisCACv91gKqKir9VisBgP%2BAgAEAAQCAgP7UKysrAAAAAQAAAAEAANV4zkFfDzz1AAMEAP%2F%2F%2F%2F%2FWOhNz%2F%2F%2F%2F%2F9Y6E3MAAP8gBIADqwAAAAoAAgABAAAAAAABAAAD6P9qAAAXcAAA%2F7YEgAABAAAAAAAAAAAAAAAAAAAAAwNSAFUDVgCABQAAgQAAAAAAAAAoAAAAsgAAAYoAAQAAAAMAXgAFAAAAAAACAIAEAAAAAAAEAADeAAAAAAAAABUBAgAAAAAAAAABABIAAAAAAAAAAAACAA4AEgAAAAAAAAADADAAIAAAAAAAAAAEABIAUAAAAAAAAAAFABYAYgAAAAAAAAAGAAkAeAAAAAAAAAAIABwAgQABAAAAAAABABIAAAABAAAAAAACAA4AEgABAAAAAAADADAAIAABAAAAAAAEABIAUAABAAAAAAAFABYAYgABAAAAAAAGAAkAeAABAAAAAAAIABwAgQADAAEECQABABIAAAADAAEECQACAA4AEgADAAEECQADADAAIAADAAEECQAEABIAUAADAAEECQAFABYAYgADAAEECQAGAAkAeAADAAEECQAIABwAgQBNAGEAdABoACAARgBvAG4AdABSAGUAZwB1AGwAYQByAE0AYQB0AGgAcwAgAEYAbwByACAATQBvAHIAZQAgAE0AYQB0AGgAIABGAG8AbgB0AE0AYQB0AGgAIABGAG8AbgB0AFYAZQByAHMAaQBvAG4AIAAxAC4AME1hdGhfRm9udABNAGEAdABoAHMAIABGAG8AcgAgAE0AbwByAGUAAAMAAAAAAAAB9AD6AAAAAAAAAAAAAAAAAAAAAAAAAAC5BxEAAI2FGACyAAAAFRQTsQABPw%3D%3D)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'round_brackets18549f92a457f2409'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMjwHLFQAAADMAAAATmNtYXDf7xCrAAABHAAAADxjdnQgBAkDLgAAAVgAAAASZ2x5ZmAOz2cAAAFsAAABJGhlYWQOKih8AAACkAAAADZoaGVhCvgVwgAAAsgAAAAkaG10eCA6AAIAAALsAAAADGxvY2EAAARLAAAC%2BAAAABBtYXhwBIgEWQAAAwgAAAAgbmFtZXHR30MAAAMoAAACOXBvc3QDogHPAAAFZAAAACBwcmVwupWEAAAABYQAAAAHAAAGcgGQAAUAAAgACAAAAAAACAAIAAAAAAAAAQIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAo8AMGe%2F57AAAHPgGyAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACACgAKf%2F%2FAAAAKAAp%2F%2F%2F%2F2f%2FZAAEAAAAAAAAAAAFUAFYBAAAsAKgDgAAyAAcAAAACAAAAKgDVA1UAAwAHAAA1MxEjEyMRM9XVq4CAKgMr%2FQAC1QABAAD%2B0AIgBtAACQBNGAGwChCwA9SwAxCwAtSwChCwBdSwBRCwANSwAxCwBzywAhCwCDwAsAoQsAPUsAMQsAfUsAoQsAXUsAoQsADUsAMQsAI8sAcQsAg8MTAREAEzABEQASMAAZCQ%2FnABkJD%2BcALQ%2FZD%2BcAGQAnACcAGQ%2FnAAAQAA%2FtACIAbQAAkATRgBsAoQsAPUsAMQsALUsAoQsAXUsAUQsADUsAMQsAc8sAIQsAg8ALAKELAD1LADELAH1LAKELAF1LAKELAA1LADELACPLAHELAIPDEwARABIwAREAEzAAIg%2FnCQAZD%2BcJABkALQ%2FZD%2BcAGQAnACcAGQ%2FnAAAQAAAAEAAPW2NYFfDzz1AAMIAP%2F%2F%2F%2F%2FVre7u%2F%2F%2F%2F%2F9Wt7u4AAP7QA7cG0AAAAAoAAgABAAAAAAABAAAHPv5OAAAXcAAA%2F%2F4DtwABAAAAAAAAAAAAAAAAAAAAAwDVAAACIAAAAiAAAAAAAAAAAAAkAAAAowAAASQAAQAAAAMACgACAAAAAAACAIAEAAAAAAAEAABNAAAAAAAAABUBAgAAAAAAAAABAD4AAAAAAAAAAAACAA4APgAAAAAAAAADAFwATAAAAAAAAAAEAD4AqAAAAAAAAAAFABYA5gAAAAAAAAAGAB8A%2FAAAAAAAAAAIABwBGwABAAAAAAABAD4AAAABAAAAAAACAA4APgABAAAAAAADAFwATAABAAAAAAAEAD4AqAABAAAAAAAFABYA5gABAAAAAAAGAB8A%2FAABAAAAAAAIABwBGwADAAEECQABAD4AAAADAAEECQACAA4APgADAAEECQADAFwATAADAAEECQAEAD4AqAADAAEECQAFABYA5gADAAEECQAGAB8A%2FAADAAEECQAIABwBGwBSAG8AdQBuAGQAIABiAHIAYQBjAGsAZQB0AHMAIAB3AGkAdABoACAAYQBzAGMAZQBuAHQAIAAxADgANQA0AFIAZQBnAHUAbABhAHIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlACAAUgBvAHUAbgBkACAAYgByAGEAYwBrAGUAdABzACAAdwBpAHQAaAAgAGEAcwBjAGUAbgB0ACAAMQA4ADUANABSAG8AdQBuAGQAIABiAHIAYQBjAGsAZQB0AHMAIAB3AGkAdABoACAAYQBzAGMAZQBuAHQAIAAxADgANQA0AFYAZQByAHMAaQBvAG4AIAAyAC4AMFJvdW5kX2JyYWNrZXRzX3dpdGhfYXNjZW50XzE4NTQATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlAAAAAAMAAAAAAAADnwHPAAAAAAAAAAAAAAAAAAAAAAAAAAC5B%2F8AAY2FAA%3D%3D)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2211.5%22%20y%3D%2234%22%3Em%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1d8b8eed422c106ae9d7c55579f%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%2245.5%22%20y%3D%2234%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%2271.5%22%20y%3D%2234%22%3E(%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2282.5%22%20y%3D%2234%22%3Eb%3C%2Ftext%3E%3Ctext%20font-family%3D%22ae2ef524fbf3d9fe611d5a8e90fefdc%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2296.5%22%20y%3D%2234%22%3Ea%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22109.5%22%20y%3D%2234%22%3Es%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22123.5%22%20y%3D%2234%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22135.5%22%20y%3D%2234%22%3E)%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22148.5%22%20y%3D%2224%22%3En%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1d8b8eed422c106ae9d7c55579f%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22176.5%22%20y%3D%2234%22%3E%26%23x21D4%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22203.5%22%20y%3D%2234%22%3En%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1d8b8eed422c106ae9d7c55579f%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22233.5%22%20y%3D%2234%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22264.5%22%20y%3D%2234%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22287.5%22%20y%3D%2252%22%3E(%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22298.5%22%20y%3D%2252%22%3Eb%3C%2Ftext%3E%3Ctext%20font-family%3D%22ae2ef524fbf3d9fe611d5a8e90fefdc%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22312.5%22%20y%3D%2252%22%3Ea%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22325.5%22%20y%3D%2252%22%3Es%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22339.5%22%20y%3D%2252%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22351.5%22%20y%3D%2252%22%3E)%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22368.5%22%20y%3D%2234%22%3Em%3C%2Ftext%3E%3C%2Fsvg%3E)
Cependant, sur les calculatrices conventionnelles, on ne peut évaluer

et c'est à ce moment que l'on utilise la formule de changement de base :
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'math17f39f8317fbdb1988ef4c628eb'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAADRjdnQgDVUNBwAAAVAAAAA6Z2x5ZoPi2VsAAAGMAAAAsmhlYWQQC2qxAAACQAAAADZoaGVhCGsXSAAAAngAAAAkaG10eE2rRkcAAAKcAAAACGxvY2EAHTwYAAACpAAAAAxtYXhwBT0FPgAAArAAAAAgbmFtZaBxlY4AAALQAAABn3Bvc3QB9wD6AAAEcAAAACBwcmVwa1uragAABJAAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACAAAAAEAAQAAQAAAD3%2F%2FwAAAD3%2F%2F%2F%2FEAAEAAAAAAAABVAMsAIABAABWACoCWAIeAQ4BLAIsAFoBgAKAAKAA1ACAAAAAAAAAACsAVQCAAKsA1QEAASsABwAAAAIAVQAAAwADqwADAAcAADMRIRElIREhVQKr%2FasCAP4AA6v8VVUDAAACAIAA6wLVAhUAAwAHAGUYAbAIELAG1LAGELAF1LAIELAB1LABELAA1LAGELAHPLAFELAEPLABELACPLAAELADPACwCBCwBtSwBhCwB9SwBxCwAdSwARCwAtSwBhCwBTywBxCwBDywARCwADywAhCwAzwxMBMhNSEdASE1gAJV%2FasCVQHAVdVVVQAAAAEAAAABAADVeM5BXw889QADBAD%2F%2F%2F%2F%2F1joTc%2F%2F%2F%2F%2F%2FWOhNzAAD%2FIASAA6sAAAAKAAIAAQAAAAAAAQAAA%2Bj%2FagAAF3AAAP%2B2BIAAAQAAAAAAAAAAAAAAAAAAAAIDUgBVA1YAgAAAAAAAAAAoAAAAsgABAAAAAgBeAAUAAAAAAAIAgAQAAAAAAAQAAN4AAAAAAAAAFQECAAAAAAAAAAEAEgAAAAAAAAAAAAIADgASAAAAAAAAAAMAMAAgAAAAAAAAAAQAEgBQAAAAAAAAAAUAFgBiAAAAAAAAAAYACQB4AAAAAAAAAAgAHACBAAEAAAAAAAEAEgAAAAEAAAAAAAIADgASAAEAAAAAAAMAMAAgAAEAAAAAAAQAEgBQAAEAAAAAAAUAFgBiAAEAAAAAAAYACQB4AAEAAAAAAAgAHACBAAMAAQQJAAEAEgAAAAMAAQQJAAIADgASAAMAAQQJAAMAMAAgAAMAAQQJAAQAEgBQAAMAAQQJAAUAFgBiAAMAAQQJAAYACQB4AAMAAQQJAAgAHACBAE0AYQB0AGgAIABGAG8AbgB0AFIAZQBnAHUAbABhAHIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlACAATQBhAHQAaAAgAEYAbwBuAHQATQBhAHQAaAAgAEYAbwBuAHQAVgBlAHIAcwBpAG8AbgAgADEALgAwTWF0aF9Gb250AE0AYQB0AGgAcwAgAEYAbwByACAATQBvAHIAZQAAAwAAAAAAAAH0APoAAAAAAAAAAAAAAAAAAAAAAAAAALkHEQAAjYUYALIAAAAVFBOxAAE%2F)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2224%22%20text-anchor%3D%22middle%22%20x%3D%2216.5%22%20y%3D%2246%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22ae2ef524fbf3d9fe611d5a8e90fefdc%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2237.5%22%20y%3D%2253%22%3Ea%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2224%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2256.5%22%20y%3D%2246%22%3Ec%3C%2Ftext%3E%3Ctext%20font-family%3D%22math17f39f8317fbdb1988ef4c628eb%22%20font-size%3D%2224%22%20text-anchor%3D%22middle%22%20x%3D%2276.5%22%20y%3D%2246%22%3E%3D%3C%2Ftext%3E%3Cline%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%2292.5%22%20x2%3D%22169.5%22%20y1%3D%2237.5%22%20y2%3D%2237.5%22%2F%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2224%22%20text-anchor%3D%22middle%22%20x%3D%22111.5%22%20y%3D%2223%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%22137.5%22%20y%3D%2230%22%3E10%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2224%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22160.5%22%20y%3D%2223%22%3Ec%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2224%22%20text-anchor%3D%22middle%22%20x%3D%22112.5%22%20y%3D%2262%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%22138.5%22%20y%3D%2270%22%3E10%3C%2Ftext%3E%3Ctext%20font-family%3D%22ae2ef524fbf3d9fe611d5a8e90fefdc%22%20font-size%3D%2224%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22159.5%22%20y%3D%2262%22%3Ea%3C%2Ftext%3E%3C%2Fsvg%3E)
d'où
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%225.5%22%20y%3D%2220%22%3Ex%3C%2Ftext%3E%3Ctext%20font-family%3D%22math17f39f8317fbdb1988ef4c628eb%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%2221.5%22%20y%3D%2220%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%2245.5%22%20y%3D%2220%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2215%22%20text-anchor%3D%22middle%22%20x%3D%2263.5%22%20y%3D%2226%22%3E5%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%2283.5%22%20y%3D%2220%22%3E202%3C%2Ftext%3E%3C%2Fsvg%3E)
devient
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%225.5%22%20y%3D%2236%22%3Ex%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1441a2c6ef28893a9f43fb56770%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%2221.5%22%20y%3D%2236%22%3E%3D%3C%2Ftext%3E%3Cline%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%2234.5%22%20x2%3D%22115.5%22%20y1%3D%2229.5%22%20y2%3D%2229.5%22%2F%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%2250.5%22%20y%3D%2218%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2215%22%20text-anchor%3D%22middle%22%20x%3D%2272.5%22%20y%3D%2224%22%3E10%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%2296.5%22%20y%3D%2218%22%3E202%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%2261.5%22%20y%3D%2249%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2215%22%20text-anchor%3D%22middle%22%20x%3D%2283.5%22%20y%3D%2255%22%3E10%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%2296.5%22%20y%3D%2249%22%3E5%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1441a2c6ef28893a9f43fb56770%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%22128.5%22%20y%3D%2236%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%22144.5%22%20y%3D%2236%22%3E3%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1441a2c6ef28893a9f43fb56770%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%22153.5%22%20y%3D%2236%22%3E%2C%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%22178.5%22%20y%3D%2236%22%3E2982%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1441a2c6ef28893a9f43fb56770%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%22203.5%22%20y%3D%2236%22%3E.%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1441a2c6ef28893a9f43fb56770%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%22209.5%22%20y%3D%2236%22%3E.%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1441a2c6ef28893a9f43fb56770%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%22215.5%22%20y%3D%2236%22%3E.%3C%2Ftext%3E%3C%2Fsvg%3E)
Ainsi, 3,2982 est la valeur que l'on doit affecter comme exposant à 5 pour obtenir 202 comme puissance.
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%225.5%22%20y%3D%2223%22%3E5%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2215%22%20text-anchor%3D%22middle%22%20x%3D%2215.5%22%20y%3D%2215%22%3E3%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1e080d427c4d377ecbc02e4482b%22%20font-size%3D%2215%22%20text-anchor%3D%22middle%22%20x%3D%2221.5%22%20y%3D%2215%22%3E%2C%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2215%22%20text-anchor%3D%22middle%22%20x%3D%2240.5%22%20y%3D%2215%22%3E2982%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1e080d427c4d377ecbc02e4482b%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%2266.5%22%20y%3D%2223%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%2293.5%22%20y%3D%2223%22%3E201%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1e080d427c4d377ecbc02e4482b%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%22113.5%22%20y%3D%2223%22%3E%2C%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2220%22%20text-anchor%3D%22middle%22%20x%3D%22149.5%22%20y%3D%2223%22%3E996046%3C%2Ftext%3E%3C%2Fsvg%3E)
P.S. On n'obtient pas précisément 202 car on a oublié volontairement les chiffres après les dix-millièmes dans 3,298212162....
Fais les exercices ci-dessous. |
|
 La fonction logarithmique La fonction logarithmique |
La fonction logarithmique
Cette fonction est la réciproque d'une fonction exponentielle.
Il s'agit d'une fonction dont la règle est :
%3C%2Fmo%3E%3Cmo%3E%3D%3C%2Fmo%3E%3Cmi%3Ea%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmsub%3E%3Cmi%3Elog%3C%2Fmi%3E%3Cmrow%3E%3Cmo%3E(%3C%2Fmo%3E%3Cmi%3Eb%3C%2Fmi%3E%3Cmi%3Ea%3C%2Fmi%3E%3Cmi%3Es%3C%2Fmi%3E%3Cmi%3Ee%3C%2Fmi%3E%3Cmo%3E)%3C%2Fmo%3E%3C%2Fmrow%3E%3C%2Fmsub%3E%3Cmi%3Eb%3C%2Fmi%3E%3Cmi%3Ex%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmo%3E%2C%3C%2Fmo%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%3Eo%3C%2Fmi%3E%3Cmi%3Eu%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%3Ea%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmo%3E%26%23x2260%3B%3C%2Fmo%3E%3Cmn%3E0%3C%2Fmn%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmo%3E%2C%3C%2Fmo%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%3Eb%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmo%3E%26%23x2260%3B%3C%2Fmo%3E%3Cmn%3E0%3C%2Fmn%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%3Ee%3C%2Fmi%3E%3Cmi%3Et%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%3Eo%3C%2Fmi%3E%3Cmi%3E%26%23xF9%3B%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%3El%3C%2Fmi%3E%3Cmi%3Ea%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%3Eb%3C%2Fmi%3E%3Cmi%3Ea%3C%2Fmi%3E%3Cmi%3Es%3C%2Fmi%3E%3Cmi%3Ee%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%3Ee%3C%2Fmi%3E%3Cmi%3Es%3C%2Fmi%3E%3Cmi%3Et%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%3Es%3C%2Fmi%3E%3Cmi%3Eu%3C%2Fmi%3E%3Cmi%3Ep%3C%2Fmi%3E%3Cmi%3E%26%23xE9%3B%3C%2Fmi%3E%3Cmi%3Er%3C%2Fmi%3E%3Cmi%3Ei%3C%2Fmi%3E%3Cmi%3Ee%3C%2Fmi%3E%3Cmi%3Eu%3C%2Fmi%3E%3Cmi%3Er%3C%2Fmi%3E%3Cmi%3Ee%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%3E%26%23xE0%3B%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmn%3E0%3C%2Fmn%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%3Ee%3C%2Fmi%3E%3Cmi%3Et%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%3Ed%3C%2Fmi%3E%3Cmi%3Ei%3C%2Fmi%3E%3Cmi%3Ef%3C%2Fmi%3E%3Cmi%3Ef%3C%2Fmi%3E%3Cmi%3E%26%23xE9%3B%3C%2Fmi%3E%3Cmi%3Er%3C%2Fmi%3E%3Cmi%3Ee%3C%2Fmi%3E%3Cmi%3En%3C%2Fmi%3E%3Cmi%3Et%3C%2Fmi%3E%3Cmi%3Ee%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmi%3Ed%3C%2Fmi%3E%3Cmi%3Ee%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmn%3E1%3C%2Fmn%3E%3Cmo%3E.%3C%2Fmo%3E%3C%2Fmath%3E--%3E%3Cdefs%3E%3Cstyle%20type%3D%22text%2Fcss%22%3E%40font-face%7Bfont-family%3A'a9ae65dcc5ba03ef2f0f633c7df668a'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMjv%2FLJYAAADMAAAATmNtYXDgWxEdAAABHAAAADxjdnQgAAAABwAAAVgAAAAEZ2x5ZoYrxVAAAAFcAAABW2hlYWQOdyayAAACuAAAADZoaGVhC0UVwQAAAvAAAAAkaG10eCg8AIUAAAMUAAAADGxvY2EAAAVKAAADIAAAABBtYXhwBIoEWwAAAzAAAAAgbmFtZXSF9ZsAAANQAAABrXBvc3QDogHPAAAFAAAAACBwcmVwukanGAAABSAAAAANAAAGtAGQAAUAAAgACAAAAAAACAAIAAAAAAAAAQIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg8AMGe%2F57AAAHPgGyAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACAGEAZv%2F%2FAAAAYQBm%2F%2F%2F%2FoP%2BcAAEAAAAAAAAAAAAHAAIAVQAAAwADqwADAAcAADMRIRElIREhVQKr%2FasCAP4AA6v8VVUDAAADAC3%2FdAQDBFkACwAXAB0AOxgBsB0QsAPUsAMQsBTUsBQQsBzUsBwQsAnUsBwQsA48sAkQsBs8ALAGELAR1LAGELAA1LAAELAX1DAxASIAERYSMzISNxAmBhYDAgYjIiY1NDYzATUGEyMSAgGz%2Ft8W9bLTugOFhnAWDE6FWbKyhQHtjASyUQRZ%2Ft%2F%2B3vX%2B3wEz4wGnnLIt%2Fp3%2FAGXInN%2By%2FFmMXQHn%2FV4AAQAB%2FvUC9QZDABoANRgBsBsQsAjUsAgQsAHUsBsQsAzUsAwQsBjUALAbELAK1LAKELAL1LAbELAA1LAAELAY1DAxAREQIyInNRY3ESM3FzUQITIXFSYjIgYdASEVAWXfWSyxAYYDgwFkWYVZWVmFAQsDp%2FxZ%2FvUshlmyA6eHAYUBkVmGWVmyhYYAAAEAAAABAACav9usXw889QADCAD%2F%2F%2F%2F%2F1a3uPf%2F%2F%2F%2F%2FVre49AAH%2B9QQDBkMAAAAKAAIAAQAAAAAAAQAABz7%2BTgAAF3AAAf%2F8BAMAAQAAAAAAAAAAAAAAAAAAAAMDUgBVBEwALQLxAAEAAAAAAAAAKAAAANEAAAFbAAEAAAADAB4AAwAAAAAAAgCABAAAAAAABAAAOwAAAAAAAAAVAQIAAAAAAAAAAQAWAAAAAAAAAAAAAgAOABYAAAAAAAAAAwA0ACQAAAAAAAAABAAWAFgAAAAAAAAABQAWAG4AAAAAAAAABgALAIQAAAAAAAAACAAcAI8AAQAAAAAAAQAWAAAAAQAAAAAAAgAOABYAAQAAAAAAAwA0ACQAAQAAAAAABAAWAFgAAQAAAAAABQAWAG4AAQAAAAAABgALAIQAAQAAAAAACAAcAI8AAwABBAkAAQAWAAAAAwABBAkAAgAOABYAAwABBAkAAwA0ACQAAwABBAkABAAWAFgAAwABBAkABQAWAG4AAwABBAkABgALAIQAAwABBAkACAAcAI8ATQBhAHQAaAAgAEYAbwBuAHQAIAAyAFIAZQBnAHUAbABhAHIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlACAATQBhAHQAaAAgAEYAbwBuAHQAIAAyAE0AYQB0AGgAIABGAG8AbgB0ACAAMgBWAGUAcgBzAGkAbwBuACAAMQAuADBNYXRoX0ZvbnRfMgBNAGEAdABoAHMAIABGAG8AcgAgAE0AbwByAGUAAAAAAwAAAAAAAAOfAc8AAAAAAAAAAAAAAAAAAAAAAAAAALkHIgAAjYUYALIAAAAAAAA%3D)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'math192adcc127bfff5dc15e083854e'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAAExjdnQgDVUNBwAAAWgAAAA6Z2x5ZoPi2VsAAAGkAAABvmhlYWQQC2qxAAADZAAAADZoaGVhCGsXSAAAA5wAAAAkaG10eE2rRkcAAAPAAAAAFGxvY2EAHTwYAAAD1AAAABhtYXhwBT0FPgAAA%2BwAAAAgbmFtZaBxlY4AAAQMAAABn3Bvc3QB9wD6AAAFrAAAACBwcmVwa1uragAABcwAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEADgAAAAKAAgAAgACACwALgA9ImD%2F%2FwAAACwALgA9ImD%2F%2F%2F%2FV%2F9T%2Fxt2kAAEAAAAAAAAAAAAAAAABVAMsAIABAABWACoCWAIeAQ4BLAIsAFoBgAKAAKAA1ACAAAAAAAAAACsAVQCAAKsA1QEAASsABwAAAAIAVQAAAwADqwADAAcAADMRIRElIREhVQKr%2FasCAP4AA6v8VVUDAAABAFX%2FZADVAIAACgAAMzUzFRQGByc%2BATdVgC8vGx4eAYB6PVEUKQ40MQABACAAAACgAIAAAwAvGAGwBBCwA9SwAxCwAtSwAxCwADywAhCwATwAsAQQsAPUsAMQsAI8sAAQsAE8MDE3MxUjIICAgIAAAgCAAOsC1QIVAAMABwBlGAGwCBCwBtSwBhCwBdSwCBCwAdSwARCwANSwBhCwBzywBRCwBDywARCwAjywABCwAzwAsAgQsAbUsAYQsAfUsAcQsAHUsAEQsALUsAYQsAU8sAcQsAQ8sAEQsAA8sAIQsAM8MTATITUhHQEhNYACVf2rAlUBwFXVVVUAAwCAAHMC1QKPAAMABwALAGUYAbAMELAG1LAGELAF1LAMELAB1LABELAA1LAGELAHPLAFELAEPLABELACPLAAELADPACwDBCwBtSwBhCwB9SwBxCwAdSwARCwAtSwBhCwBTywBxCwBDywARCwADywAhCwAzwxMBMhNSEdASE1AwEzAYACVf2rAlV%2F%2FlZVAasBwFXVVVUBT%2F3kAhwAAAABAAAAAQAA1XjOQV8PPPUAAwQA%2F%2F%2F%2F%2F9Y6E3P%2F%2F%2F%2F%2F1joTcwAA%2FyAEgAOrAAAACgACAAEAAAAAAAEAAAPo%2F2oAABdwAAD%2FtgSAAAEAAAAAAAAAAAAAAAAAAAAFA1IAVQEzAFUAyAAgA1YAgANWAIAAAAAAAAAAKAAAAFIAAACYAAABIgAAAb4AAQAAAAUAXgAFAAAAAAACAIAEAAAAAAAEAADeAAAAAAAAABUBAgAAAAAAAAABABIAAAAAAAAAAAACAA4AEgAAAAAAAAADADAAIAAAAAAAAAAEABIAUAAAAAAAAAAFABYAYgAAAAAAAAAGAAkAeAAAAAAAAAAIABwAgQABAAAAAAABABIAAAABAAAAAAACAA4AEgABAAAAAAADADAAIAABAAAAAAAEABIAUAABAAAAAAAFABYAYgABAAAAAAAGAAkAeAABAAAAAAAIABwAgQADAAEECQABABIAAAADAAEECQACAA4AEgADAAEECQADADAAIAADAAEECQAEABIAUAADAAEECQAFABYAYgADAAEECQAGAAkAeAADAAEECQAIABwAgQBNAGEAdABoACAARgBvAG4AdABSAGUAZwB1AGwAYQByAE0AYQB0AGgAcwAgAEYAbwByACAATQBvAHIAZQAgAE0AYQB0AGgAIABGAG8AbgB0AE0AYQB0AGgAIABGAG8AbgB0AFYAZQByAHMAaQBvAG4AIAAxAC4AME1hdGhfRm9udABNAGEAdABoAHMAIABGAG8AcgAgAE0AbwByAGUAAAMAAAAAAAAB9AD6AAAAAAAAAAAAAAAAAAAAAAAAAAC5BxEAAI2FGACyAAAAFRQTsQABPw%3D%3D)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'round_brackets18549f92a457f2409'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMjwHLFQAAADMAAAATmNtYXDf7xCrAAABHAAAADxjdnQgBAkDLgAAAVgAAAASZ2x5ZmAOz2cAAAFsAAABJGhlYWQOKih8AAACkAAAADZoaGVhCvgVwgAAAsgAAAAkaG10eCA6AAIAAALsAAAADGxvY2EAAARLAAAC%2BAAAABBtYXhwBIgEWQAAAwgAAAAgbmFtZXHR30MAAAMoAAACOXBvc3QDogHPAAAFZAAAACBwcmVwupWEAAAABYQAAAAHAAAGcgGQAAUAAAgACAAAAAAACAAIAAAAAAAAAQIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAo8AMGe%2F57AAAHPgGyAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACACgAKf%2F%2FAAAAKAAp%2F%2F%2F%2F2f%2FZAAEAAAAAAAAAAAFUAFYBAAAsAKgDgAAyAAcAAAACAAAAKgDVA1UAAwAHAAA1MxEjEyMRM9XVq4CAKgMr%2FQAC1QABAAD%2B0AIgBtAACQBNGAGwChCwA9SwAxCwAtSwChCwBdSwBRCwANSwAxCwBzywAhCwCDwAsAoQsAPUsAMQsAfUsAoQsAXUsAoQsADUsAMQsAI8sAcQsAg8MTAREAEzABEQASMAAZCQ%2FnABkJD%2BcALQ%2FZD%2BcAGQAnACcAGQ%2FnAAAQAA%2FtACIAbQAAkATRgBsAoQsAPUsAMQsALUsAoQsAXUsAUQsADUsAMQsAc8sAIQsAg8ALAKELAD1LADELAH1LAKELAF1LAKELAA1LADELACPLAHELAIPDEwARABIwAREAEzAAIg%2FnCQAZD%2BcJABkALQ%2FZD%2BcAGQAnACcAGQ%2FnAAAQAAAAEAAPW2NYFfDzz1AAMIAP%2F%2F%2F%2F%2FVre7u%2F%2F%2F%2F%2F9Wt7u4AAP7QA7cG0AAAAAoAAgABAAAAAAABAAAHPv5OAAAXcAAA%2F%2F4DtwABAAAAAAAAAAAAAAAAAAAAAwDVAAACIAAAAiAAAAAAAAAAAAAkAAAAowAAASQAAQAAAAMACgACAAAAAAACAIAEAAAAAAAEAABNAAAAAAAAABUBAgAAAAAAAAABAD4AAAAAAAAAAAACAA4APgAAAAAAAAADAFwATAAAAAAAAAAEAD4AqAAAAAAAAAAFABYA5gAAAAAAAAAGAB8A%2FAAAAAAAAAAIABwBGwABAAAAAAABAD4AAAABAAAAAAACAA4APgABAAAAAAADAFwATAABAAAAAAAEAD4AqAABAAAAAAAFABYA5gABAAAAAAAGAB8A%2FAABAAAAAAAIABwBGwADAAEECQABAD4AAAADAAEECQACAA4APgADAAEECQADAFwATAADAAEECQAEAD4AqAADAAEECQAFABYA5gADAAEECQAGAB8A%2FAADAAEECQAIABwBGwBSAG8AdQBuAGQAIABiAHIAYQBjAGsAZQB0AHMAIAB3AGkAdABoACAAYQBzAGMAZQBuAHQAIAAxADgANQA0AFIAZQBnAHUAbABhAHIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlACAAUgBvAHUAbgBkACAAYgByAGEAYwBrAGUAdABzACAAdwBpAHQAaAAgAGEAcwBjAGUAbgB0ACAAMQA4ADUANABSAG8AdQBuAGQAIABiAHIAYQBjAGsAZQB0AHMAIAB3AGkAdABoACAAYQBzAGMAZQBuAHQAIAAxADgANQA0AFYAZQByAHMAaQBvAG4AIAAyAC4AMFJvdW5kX2JyYWNrZXRzX3dpdGhfYXNjZW50XzE4NTQATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlAAAAAAMAAAAAAAADnwHPAAAAAAAAAAAAAAAAAAAAAAAAAAC5B%2F8AAY2FAA%3D%3D)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22a9ae65dcc5ba03ef2f0f633c7df668a%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%223.5%22%20y%3D%2216%22%3Ef%3C%2Ftext%3E%3Ctext%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2212.5%22%20y%3D%2216%22%3E(%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2218.5%22%20y%3D%2216%22%3Ex%3C%2Ftext%3E%3Ctext%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2225.5%22%20y%3D%2216%22%3E)%3C%2Ftext%3E%3Ctext%20font-family%3D%22math192adcc127bfff5dc15e083854e%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2236.5%22%20y%3D%2216%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22a9ae65dcc5ba03ef2f0f633c7df668a%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2249.5%22%20y%3D%2216%22%3Ea%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2269.5%22%20y%3D%2216%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2212%22%20text-anchor%3D%22middle%22%20x%3D%2282.5%22%20y%3D%2221%22%3E(%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2287.5%22%20y%3D%2221%22%3Eb%3C%2Ftext%3E%3Ctext%20font-family%3D%22a9ae65dcc5ba03ef2f0f633c7df668a%22%20font-size%3D%2212%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2294.5%22%20y%3D%2221%22%3Ea%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22100.5%22%20y%3D%2221%22%3Es%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22106.5%22%20y%3D%2221%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2212%22%20text-anchor%3D%22middle%22%20x%3D%22112.5%22%20y%3D%2221%22%3E)%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22119.5%22%20y%3D%2216%22%3Eb%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22128.5%22%20y%3D%2216%22%3Ex%3C%2Ftext%3E%3Ctext%20font-family%3D%22math192adcc127bfff5dc15e083854e%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22139.5%22%20y%3D%2216%22%3E%2C%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22150.5%22%20y%3D%2216%22%3Eo%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22159.5%22%20y%3D%2216%22%3Eu%3C%2Ftext%3E%3Ctext%20font-family%3D%22a9ae65dcc5ba03ef2f0f633c7df668a%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22173.5%22%20y%3D%2216%22%3Ea%3C%2Ftext%3E%3Ctext%20font-family%3D%22math192adcc127bfff5dc15e083854e%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22191.5%22%20y%3D%2216%22%3E%26%23x2260%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22204.5%22%20y%3D%2216%22%3E0%3C%2Ftext%3E%3Ctext%20font-family%3D%22math192adcc127bfff5dc15e083854e%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22215.5%22%20y%3D%2216%22%3E%2C%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22226.5%22%20y%3D%2216%22%3Eb%3C%2Ftext%3E%3Ctext%20font-family%3D%22math192adcc127bfff5dc15e083854e%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22244.5%22%20y%3D%2216%22%3E%26%23x2260%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22257.5%22%20y%3D%2216%22%3E0%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22270.5%22%20y%3D%2216%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22277.5%22%20y%3D%2216%22%3Et%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22288.5%22%20y%3D%2216%22%3Eo%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22297.5%22%20y%3D%2216%22%3E%26%23xF9%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22309.5%22%20y%3D%2216%22%3El%3C%2Ftext%3E%3Ctext%20font-family%3D%22a9ae65dcc5ba03ef2f0f633c7df668a%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22315.5%22%20y%3D%2216%22%3Ea%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22329.5%22%20y%3D%2216%22%3Eb%3C%2Ftext%3E%3Ctext%20font-family%3D%22a9ae65dcc5ba03ef2f0f633c7df668a%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22338.5%22%20y%3D%2216%22%3Ea%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22347.5%22%20y%3D%2216%22%3Es%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22355.5%22%20y%3D%2216%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22369.5%22%20y%3D%2216%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22378.5%22%20y%3D%2216%22%3Es%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22384.5%22%20y%3D%2216%22%3Et%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22395.5%22%20y%3D%2216%22%3Es%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22403.5%22%20y%3D%2216%22%3Eu%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22412.5%22%20y%3D%2216%22%3Ep%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22421.5%22%20y%3D%2216%22%3E%26%23xE9%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22428.5%22%20y%3D%2216%22%3Er%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22433.5%22%20y%3D%2216%22%3Ei%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22439.5%22%20y%3D%2216%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22448.5%22%20y%3D%2216%22%3Eu%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22455.5%22%20y%3D%2216%22%3Er%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22462.5%22%20y%3D%2216%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22476.5%22%20y%3D%2216%22%3E%26%23xE0%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22490.5%22%20y%3D%2216%22%3E0%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22503.5%22%20y%3D%2216%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22510.5%22%20y%3D%2216%22%3Et%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22521.5%22%20y%3D%2216%22%3Ed%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22528.5%22%20y%3D%2216%22%3Ei%3C%2Ftext%3E%3Ctext%20font-family%3D%22a9ae65dcc5ba03ef2f0f633c7df668a%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22533.5%22%20y%3D%2216%22%3Ef%3C%2Ftext%3E%3Ctext%20font-family%3D%22a9ae65dcc5ba03ef2f0f633c7df668a%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22541.5%22%20y%3D%2216%22%3Ef%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22550.5%22%20y%3D%2216%22%3E%26%23xE9%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22557.5%22%20y%3D%2216%22%3Er%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22564.5%22%20y%3D%2216%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22573.5%22%20y%3D%2216%22%3En%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22580.5%22%20y%3D%2216%22%3Et%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22586.5%22%20y%3D%2216%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22600.5%22%20y%3D%2216%22%3Ed%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22609.5%22%20y%3D%2216%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22623.5%22%20y%3D%2216%22%3E1%3C%2Ftext%3E%3Ctext%20font-family%3D%22math192adcc127bfff5dc15e083854e%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22630.5%22%20y%3D%2216%22%3E.%3C%2Ftext%3E%3C%2Fsvg%3E)
La représentation graphique est une courbe :
-
- passant par le point
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'brack_sm2882ad605b1e27be87c7468'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7PH4UAAADMAAAATmNtYXA3kjw6AAABHAAAADxjdnQgAQYDiAAAAVgAAAASZ2x5ZkyYQ7YAAAFsAAAAkWhlYWQLyR8fAAACAAAAADZoaGVhAq0XCAAAAjgAAAAkaG10eDEjA%2FUAAAJcAAAADGxvY2EAAEKZAAACaAAAABBtYXhwBJsEcQAAAngAAAAgbmFtZW7QvZAAAAKYAAAB5XBvc3QArQBVAAAEgAAAACBwcmVwu5WEAAAABKAAAAAHAAACDAGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg9AMD%2FP%2F8AAABVAABAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACI5wjn%2F%2F%2FAAAjnCOf%2F%2F%2FcZdxjAAEAAAAAAAAAAAFUAFQBAAArAIwAgACoAAcAAAACAAAAAADVAQEAAwAHAAAxMxEjFyM1M9XVq4CAAQHWqwABAAAAAABVAVgAAwAfGAGwAy%2BwADyxAgL1sAE8ALEDAD%2BwAjx8sQAG9bABPBEzESNVVQFY%2FqgAAQDXAAABLAFUAAMAIBgBsAUvsAE8sAI8sQAC9bADPACwAy%2BwAjyxAAH1sAE8EzMRI9dVVQFU%2FqwAAAAAAQAAAAEAAIsesexfDzz1AAMEAP%2F%2F%2F%2F%2FVre5k%2F%2F%2F%2F%2F9Wt7mT%2FgP%2F%2FAdYBWAAAAAoAAgABAAAAAAABAAABVP%2F%2FAAAXcP%2BA%2F4AB1gABAAAAAAAAAAAAAAAAAAAAAwDVAAABLAAAASwA1wAAAAAAAAAhAAAAWAAAAJEAAQAAAAMACgACAAAAAAACAIAEAAAAAAAEAABlAAAAAAAAABUBAgAAAAAAAAABACYAAAAAAAAAAAACAA4AJgAAAAAAAAADAEQANAAAAAAAAAAEACYAeAAAAAAAAAAFABYAngAAAAAAAAAGABMAtAAAAAAAAAAIABwAxwABAAAAAAABACYAAAABAAAAAAACAA4AJgABAAAAAAADAEQANAABAAAAAAAEACYAeAABAAAAAAAFABYAngABAAAAAAAGABMAtAABAAAAAAAIABwAxwADAAEECQABACYAAAADAAEECQACAA4AJgADAAEECQADAEQANAADAAEECQAEACYAeAADAAEECQAFABYAngADAAEECQAGABMAtAADAAEECQAIABwAxwBCAHIAYQBjAGsAZQB0AHMAIABzAG0AYQBsAGwAIABzAGkAegBlAFIAZQBnAHUAbABhAHIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlACAAQgByAGEAYwBrAGUAdABzACAAcwBtAGEAbABsACAAcwBpAHoAZQBCAHIAYQBjAGsAZQB0AHMAIABzAG0AYQBsAGwAIABzAGkAegBlAFYAZQByAHMAaQBvAG4AIAAyAC4AMEJyYWNrZXRzX3NtYWxsX3NpemUATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlAAAAAAMAAAAAAAAAqgBVAAAAAAAAAAAAAAAAAAAAAAAAAAC5B%2F8AAo2FAA%3D%3D)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'bracketse552f5417ff4680c6b50499'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7RIisAAADMAAAATmNtYXBi7uzYAAABHAAAAExjdnQgBAkDLgAAAWgAAAASZ2x5Zo64f%2BkAAAF8AAABSWhlYWQLniGcAAACyAAAADZoaGVhBK4XLAAAAwAAAAAkaG10eCWq%2F90AAAMkAAAAFGxvY2EAABknAAADOAAAABhtYXhwBJIESAAAA1AAAAAgbmFtZRAA8I4AAANwAAAB3nBvc3QBwwDgAAAFUAAAACBwcmVwupWEAAAABXAAAAAHAAACggGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg9AMEAAAAAAADgAAAAAAAAAACAAEAAQAAABQAAwABAAAAFAAEADgAAAAKAAgAAgACI5sjnSOeI6D%2F%2FwAAI5sjnSOeI6D%2F%2F9xm3GXcZdxkAAEAAAAAAAAAAAAAAAABVABWAQAALACoA4AAMgAHAAAAAgAAACoA1QNVAAMABwAANTMRIxMjETPV1auAgCoDK%2F0AAtUAAQAAAAABgAOAAAUAJBgBsAAvsAPFsQEC%2FbADELEEBP0AsQAAP7ABPLEEBj%2BwAzwwMTEzEAEjAFUBKyv%2BqwH8AYT%2BqgABAAAAAAGAA4AABQAmGAGwAC6wA8WxBQL9sAMQsQIE%2FQB8sQAGPxiwBTyxAwb2sAI8MDEREgEzABMBAVQr%2FtMCA4D91v6qAYQB%2FAAB%2F6wAAAEsA4AABQAnGAGwAC%2BwBzywA8WxAQL9sAMQsQQE%2FQCxAAA%2FsAE8sQQGP7ADPDAxISMSATMAASxVAf7UKwFVAfwBhP6rAAH%2FrAAAASwDgAAFACkYAbABL7AHPLAExbEAAv2wBBCxAwT9AHyxAQY%2FsAA8GLEEAD%2BwAzwwMRMzEAEjANdV%2FqsrASsDgP3V%2FqsBhgAAAAABAAAAAQAAeuTcpl8PPPUAAwQA%2F%2F%2F%2F%2F9Wt7o7%2F%2F%2F%2F%2F1a3ujv%2BsAAABgAOAAAAACgACAAEAAAAAAAEAAAOAAAAAABdw%2F6z%2FrAGAAAEAAAAAAAAAAAAAAAAAAAAFANUAAAEsAAABLAAAASz%2FrAEs%2F6wAAAAAAAAAJAAAAGgAAACzAAAA%2FQAAAUkAAQAAAAUACAACAAAAAAACAIAEAAAAAAAEAAA%2BAAAAAAAAABUBAgAAAAAAAAABACQAAAAAAAAAAAACAA4AJAAAAAAAAAADAEIAMgAAAAAAAAAEACQAdAAAAAAAAAAFABYAmAAAAAAAAAAGABIArgAAAAAAAAAIABwAwAABAAAAAAABACQAAAABAAAAAAACAA4AJAABAAAAAAADAEIAMgABAAAAAAAEACQAdAABAAAAAAAFABYAmAABAAAAAAAGABIArgABAAAAAAAIABwAwAADAAEECQABACQAAAADAAEECQACAA4AJAADAAEECQADAEIAMgADAAEECQAEACQAdAADAAEECQAFABYAmAADAAEECQAGABIArgADAAEECQAIABwAwABCAHIAYQBjAGsAZQB0AHMAIABmAHUAbABsACAAcwBpAHoAZQBSAGUAZwB1AGwAYQByAE0AYQB0AGgAcwAgAEYAbwByACAATQBvAHIAZQAgAEIAcgBhAGMAawBlAHQAcwAgAGYAdQBsAGwAIABzAGkAegBlAEIAcgBhAGMAawBlAHQAcwAgAGYAdQBsAGwAIABzAGkAegBlAFYAZQByAHMAaQBvAG4AIAAyAC4AMEJyYWNrZXRzX2Z1bGxfc2l6ZQBNAGEAdABoAHMAIABGAG8AcgAgAE0AbwByAGUAAAADAAAAAAAAAcAA4AAAAAAAAAAAAAAAAAAAAAAAAAAAuQf%2FAAGNhQA%3D)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22bracketse552f5417ff4680c6b50499%22%20font-size%3D%2216%22%20text-anchor%3D%22start%22%20x%3D%221.5%22%20y%3D%2215%22%3E%26%23x239B%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22brack_sm2882ad605b1e27be87c7468%22%20font-size%3D%2216%22%20text-anchor%3D%22start%22%20x%3D%221.5%22%20y%3D%2220%22%3E%26%23x239C%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22brack_sm2882ad605b1e27be87c7468%22%20font-size%3D%2216%22%20text-anchor%3D%22start%22%20x%3D%221.5%22%20y%3D%2225%22%3E%26%23x239C%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22bracketse552f5417ff4680c6b50499%22%20font-size%3D%2216%22%20text-anchor%3D%22start%22%20x%3D%221.5%22%20y%3D%2239%22%3E%26%23x239D%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22bracketse552f5417ff4680c6b50499%22%20font-size%3D%2216%22%20text-anchor%3D%22start%22%20x%3D%2244.5%22%20y%3D%2215%22%3E%26%23x239E%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22brack_sm2882ad605b1e27be87c7468%22%20font-size%3D%2216%22%20text-anchor%3D%22start%22%20x%3D%2244.5%22%20y%3D%2220%22%3E%26%23x239F%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22brack_sm2882ad605b1e27be87c7468%22%20font-size%3D%2216%22%20text-anchor%3D%22start%22%20x%3D%2244.5%22%20y%3D%2225%22%3E%26%23x239F%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22bracketse552f5417ff4680c6b50499%22%20font-size%3D%2216%22%20text-anchor%3D%22start%22%20x%3D%2244.5%22%20y%3D%2239%22%3E%26%23x23A0%3B%3C%2Ftext%3E%3Cline%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%229.5%22%20x2%3D%2222.5%22%20y1%3D%2220.5%22%20y2%3D%2220.5%22%2F%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2216.5%22%20y%3D%2215%22%3E1%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2215.5%22%20y%3D%2237%22%3Eb%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1f7177163c833dff4b38fc8d287%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2227.5%22%20y%3D%2226%22%3E%2C%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2238.5%22%20y%3D%2226%22%3E0%3C%2Ftext%3E%3C%2Fsvg%3E) " "
- dont l'une des extrémités se rapproche de l'axe des ordonnées sans jamais y toucher.
Équivalences
Première équivalence
Cette équivalence permet de passer d'une forme d'écriture exponentielle à une forme logarithmique, et vice versa.
%3C%2Fmo%3E%3Cmi%3En%3C%2Fmi%3E%3C%2Fmsup%3E%3Cmo%3E%26%23x21D4%3B%3C%2Fmo%3E%3Cmi%3En%3C%2Fmi%3E%3Cmo%3E%26%23xA0%3B%3C%2Fmo%3E%3Cmo%3E%3D%3C%2Fmo%3E%3Cmsub%3E%3Cmi%3Elog%3C%2Fmi%3E%3Cmrow%3E%3Cmo%3E(%3C%2Fmo%3E%3Cmi%3Eb%3C%2Fmi%3E%3Cmi%3Ea%3C%2Fmi%3E%3Cmi%3Es%3C%2Fmi%3E%3Cmi%3Ee%3C%2Fmi%3E%3Cmo%3E)%3C%2Fmo%3E%3C%2Fmrow%3E%3C%2Fmsub%3E%3Cmi%3Em%3C%2Fmi%3E%3C%2Fmstyle%3E%3C%2Fmath%3E--%3E%3Cdefs%3E%3Cstyle%20type%3D%22text%2Fcss%22%3E%40font-face%7Bfont-family%3A'ae2ef524fbf3d9fe611d5a8e90fefdc'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMjv%2FLJYAAADMAAAATmNtYXDgWxEdAAABHAAAADRjdnQgAAAABwAAAVAAAAAEZ2x5ZoYrxVAAAAFUAAAA0WhlYWQOdyayAAACKAAAADZoaGVhC0UVwQAAAmAAAAAkaG10eCg8AIUAAAKEAAAACGxvY2EAAAVKAAACjAAAAAxtYXhwBIoEWwAAApgAAAAgbmFtZXSF9ZsAAAK4AAABrXBvc3QDogHPAAAEaAAAACBwcmVwukanGAAABIgAAAANAAAGtAGQAAUAAAgACAAAAAAACAAIAAAAAAAAAQIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg8AMGe%2F57AAAHPgGyAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACAAAAAEAAQAAQAAAGH%2F%2FwAAAGH%2F%2F%2F%2BgAAEAAAAAAAAABwACAFUAAAMAA6sAAwAHAAAzESERJSERIVUCq%2F2rAgD%2BAAOr%2FFVVAwAAAwAt%2F3QEAwRZAAsAFwAdADsYAbAdELAD1LADELAU1LAUELAc1LAcELAJ1LAcELAOPLAJELAbPACwBhCwEdSwBhCwANSwABCwF9QwMQEiABEWEjMyEjcQJgYWAwIGIyImNTQ2MwE1BhMjEgIBs%2F7fFvWy07oDhYZwFgxOhVmysoUB7YwEslEEWf7f%2Ft71%2Ft8BM%2BMBp5yyLf6d%2FwBlyJzfsvxZjF0B5%2F1eAAAAAAEAAAABAACav9usXw889QADCAD%2F%2F%2F%2F%2F1a3uPf%2F%2F%2F%2F%2FVre49AAH%2B9QQDBkMAAAAKAAIAAQAAAAAAAQAABz7%2BTgAAF3AAAf%2F8BAMAAQAAAAAAAAAAAAAAAAAAAAIDUgBVBEwALQAAAAAAAAAoAAAA0QABAAAAAgAeAAMAAAAAAAIAgAQAAAAAAAQAADsAAAAAAAAAFQECAAAAAAAAAAEAFgAAAAAAAAAAAAIADgAWAAAAAAAAAAMANAAkAAAAAAAAAAQAFgBYAAAAAAAAAAUAFgBuAAAAAAAAAAYACwCEAAAAAAAAAAgAHACPAAEAAAAAAAEAFgAAAAEAAAAAAAIADgAWAAEAAAAAAAMANAAkAAEAAAAAAAQAFgBYAAEAAAAAAAUAFgBuAAEAAAAAAAYACwCEAAEAAAAAAAgAHACPAAMAAQQJAAEAFgAAAAMAAQQJAAIADgAWAAMAAQQJAAMANAAkAAMAAQQJAAQAFgBYAAMAAQQJAAUAFgBuAAMAAQQJAAYACwCEAAMAAQQJAAgAHACPAE0AYQB0AGgAIABGAG8AbgB0ACAAMgBSAGUAZwB1AGwAYQByAE0AYQB0AGgAcwAgAEYAbwByACAATQBvAHIAZQAgAE0AYQB0AGgAIABGAG8AbgB0ACAAMgBNAGEAdABoACAARgBvAG4AdAAgADIAVgBlAHIAcwBpAG8AbgAgADEALgAwTWF0aF9Gb250XzIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlAAAAAAMAAAAAAAADnwHPAAAAAAAAAAAAAAAAAAAAAAAAAAC5ByIAAI2FGACyAAAAAAAA)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'math1d8b8eed422c106ae9d7c55579f'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAADxjdnQgDVUNBwAAAVgAAAA6Z2x5ZoPi2VsAAAGUAAABimhlYWQQC2qxAAADIAAAADZoaGVhCGsXSAAAA1gAAAAkaG10eE2rRkcAAAN8AAAADGxvY2EAHTwYAAADiAAAABBtYXhwBT0FPgAAA5gAAAAgbmFtZaBxlY4AAAO4AAABn3Bvc3QB9wD6AAAFWAAAACBwcmVwa1uragAABXgAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACAD0h1P%2F%2FAAAAPSHU%2F%2F%2F%2FxN4uAAEAAAAAAAAAAAFUAywAgAEAAFYAKgJYAh4BDgEsAiwAWgGAAoAAoADUAIAAAAAAAAAAKwBVAIAAqwDVAQABKwAHAAAAAgBVAAADAAOrAAMABwAAMxEhESUhESFVAqv9qwIA%2FgADq%2FxVVQMAAAIAgADrAtUCFQADAAcAZRgBsAgQsAbUsAYQsAXUsAgQsAHUsAEQsADUsAYQsAc8sAUQsAQ8sAEQsAI8sAAQsAM8ALAIELAG1LAGELAH1LAHELAB1LABELAC1LAGELAFPLAHELAEPLABELAAPLACELADPDEwEyE1IR0BITWAAlX9qwJVAcBV1VVVAAIAgQCBBIACgQAJAA8AjxgBsBAQsAXUsAUQsA%2FUsBEQsADUsAAQsAzUsA4QsAo8sAcQsAM8sAYQsAQ8sAkQsAE8sAgQsAI8sA0QsAs8ALAQELAE1LAEELAD1LADELAK1LAKELAO1LAOELAH1LAHELAG1LAEELABPLADELACPLAKELALPLAPELAMPLAOELANPLAHELAIPLAGELAJPDAxAQU3IRcJAQchJwEhNychBwSA%2FtUr%2FgAr%2FtYBKisCACv91gKqKir9VisBgP%2BAgAEAAQCAgP7UKysrAAAAAQAAAAEAANV4zkFfDzz1AAMEAP%2F%2F%2F%2F%2FWOhNz%2F%2F%2F%2F%2F9Y6E3MAAP8gBIADqwAAAAoAAgABAAAAAAABAAAD6P9qAAAXcAAA%2F7YEgAABAAAAAAAAAAAAAAAAAAAAAwNSAFUDVgCABQAAgQAAAAAAAAAoAAAAsgAAAYoAAQAAAAMAXgAFAAAAAAACAIAEAAAAAAAEAADeAAAAAAAAABUBAgAAAAAAAAABABIAAAAAAAAAAAACAA4AEgAAAAAAAAADADAAIAAAAAAAAAAEABIAUAAAAAAAAAAFABYAYgAAAAAAAAAGAAkAeAAAAAAAAAAIABwAgQABAAAAAAABABIAAAABAAAAAAACAA4AEgABAAAAAAADADAAIAABAAAAAAAEABIAUAABAAAAAAAFABYAYgABAAAAAAAGAAkAeAABAAAAAAAIABwAgQADAAEECQABABIAAAADAAEECQACAA4AEgADAAEECQADADAAIAADAAEECQAEABIAUAADAAEECQAFABYAYgADAAEECQAGAAkAeAADAAEECQAIABwAgQBNAGEAdABoACAARgBvAG4AdABSAGUAZwB1AGwAYQByAE0AYQB0AGgAcwAgAEYAbwByACAATQBvAHIAZQAgAE0AYQB0AGgAIABGAG8AbgB0AE0AYQB0AGgAIABGAG8AbgB0AFYAZQByAHMAaQBvAG4AIAAxAC4AME1hdGhfRm9udABNAGEAdABoAHMAIABGAG8AcgAgAE0AbwByAGUAAAMAAAAAAAAB9AD6AAAAAAAAAAAAAAAAAAAAAAAAAAC5BxEAAI2FGACyAAAAFRQTsQABPw%3D%3D)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'round_brackets18549f92a457f2409'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMjwHLFQAAADMAAAATmNtYXDf7xCrAAABHAAAADxjdnQgBAkDLgAAAVgAAAASZ2x5ZmAOz2cAAAFsAAABJGhlYWQOKih8AAACkAAAADZoaGVhCvgVwgAAAsgAAAAkaG10eCA6AAIAAALsAAAADGxvY2EAAARLAAAC%2BAAAABBtYXhwBIgEWQAAAwgAAAAgbmFtZXHR30MAAAMoAAACOXBvc3QDogHPAAAFZAAAACBwcmVwupWEAAAABYQAAAAHAAAGcgGQAAUAAAgACAAAAAAACAAIAAAAAAAAAQIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAo8AMGe%2F57AAAHPgGyAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACACgAKf%2F%2FAAAAKAAp%2F%2F%2F%2F2f%2FZAAEAAAAAAAAAAAFUAFYBAAAsAKgDgAAyAAcAAAACAAAAKgDVA1UAAwAHAAA1MxEjEyMRM9XVq4CAKgMr%2FQAC1QABAAD%2B0AIgBtAACQBNGAGwChCwA9SwAxCwAtSwChCwBdSwBRCwANSwAxCwBzywAhCwCDwAsAoQsAPUsAMQsAfUsAoQsAXUsAoQsADUsAMQsAI8sAcQsAg8MTAREAEzABEQASMAAZCQ%2FnABkJD%2BcALQ%2FZD%2BcAGQAnACcAGQ%2FnAAAQAA%2FtACIAbQAAkATRgBsAoQsAPUsAMQsALUsAoQsAXUsAUQsADUsAMQsAc8sAIQsAg8ALAKELAD1LADELAH1LAKELAF1LAKELAA1LADELACPLAHELAIPDEwARABIwAREAEzAAIg%2FnCQAZD%2BcJABkALQ%2FZD%2BcAGQAnACcAGQ%2FnAAAQAAAAEAAPW2NYFfDzz1AAMIAP%2F%2F%2F%2F%2FVre7u%2F%2F%2F%2F%2F9Wt7u4AAP7QA7cG0AAAAAoAAgABAAAAAAABAAAHPv5OAAAXcAAA%2F%2F4DtwABAAAAAAAAAAAAAAAAAAAAAwDVAAACIAAAAiAAAAAAAAAAAAAkAAAAowAAASQAAQAAAAMACgACAAAAAAACAIAEAAAAAAAEAABNAAAAAAAAABUBAgAAAAAAAAABAD4AAAAAAAAAAAACAA4APgAAAAAAAAADAFwATAAAAAAAAAAEAD4AqAAAAAAAAAAFABYA5gAAAAAAAAAGAB8A%2FAAAAAAAAAAIABwBGwABAAAAAAABAD4AAAABAAAAAAACAA4APgABAAAAAAADAFwATAABAAAAAAAEAD4AqAABAAAAAAAFABYA5gABAAAAAAAGAB8A%2FAABAAAAAAAIABwBGwADAAEECQABAD4AAAADAAEECQACAA4APgADAAEECQADAFwATAADAAEECQAEAD4AqAADAAEECQAFABYA5gADAAEECQAGAB8A%2FAADAAEECQAIABwBGwBSAG8AdQBuAGQAIABiAHIAYQBjAGsAZQB0AHMAIAB3AGkAdABoACAAYQBzAGMAZQBuAHQAIAAxADgANQA0AFIAZQBnAHUAbABhAHIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlACAAUgBvAHUAbgBkACAAYgByAGEAYwBrAGUAdABzACAAdwBpAHQAaAAgAGEAcwBjAGUAbgB0ACAAMQA4ADUANABSAG8AdQBuAGQAIABiAHIAYQBjAGsAZQB0AHMAIAB3AGkAdABoACAAYQBzAGMAZQBuAHQAIAAxADgANQA0AFYAZQByAHMAaQBvAG4AIAAyAC4AMFJvdW5kX2JyYWNrZXRzX3dpdGhfYXNjZW50XzE4NTQATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlAAAAAAMAAAAAAAADnwHPAAAAAAAAAAAAAAAAAAAAAAAAAAC5B%2F8AAY2FAA%3D%3D)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2211.5%22%20y%3D%2229%22%3Em%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1d8b8eed422c106ae9d7c55579f%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%2245.5%22%20y%3D%2229%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%2271.5%22%20y%3D%2229%22%3E(%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2282.5%22%20y%3D%2229%22%3Eb%3C%2Ftext%3E%3Ctext%20font-family%3D%22ae2ef524fbf3d9fe611d5a8e90fefdc%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2296.5%22%20y%3D%2229%22%3Ea%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22109.5%22%20y%3D%2229%22%3Es%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22123.5%22%20y%3D%2229%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22135.5%22%20y%3D%2229%22%3E)%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2219%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22146.5%22%20y%3D%2218%22%3En%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1d8b8eed422c106ae9d7c55579f%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22172.5%22%20y%3D%2229%22%3E%26%23x21D4%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22199.5%22%20y%3D%2229%22%3En%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1d8b8eed422c106ae9d7c55579f%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22229.5%22%20y%3D%2229%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22260.5%22%20y%3D%2229%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2219%22%20text-anchor%3D%22middle%22%20x%3D%22282.5%22%20y%3D%2236%22%3E(%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2219%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22289.5%22%20y%3D%2236%22%3Eb%3C%2Ftext%3E%3Ctext%20font-family%3D%22ae2ef524fbf3d9fe611d5a8e90fefdc%22%20font-size%3D%2219%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22300.5%22%20y%3D%2236%22%3Ea%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2219%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22310.5%22%20y%3D%2236%22%3Es%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2219%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22320.5%22%20y%3D%2236%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2219%22%20text-anchor%3D%22middle%22%20x%3D%22329.5%22%20y%3D%2236%22%3E)%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22344.5%22%20y%3D%2229%22%3Em%3C%2Ftext%3E%3C%2Fsvg%3E)
Exemples
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%229.5%22%20y%3D%2218%22%3E20%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1d8b8eed422c106ae9d7c55579f%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2230.5%22%20y%3D%2218%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2247.5%22%20y%3D%2218%22%3E9%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2255.5%22%20y%3D%2211%22%3Ex%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1d8b8eed422c106ae9d7c55579f%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2271.5%22%20y%3D%2218%22%3E%26%23x21D4%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2287.5%22%20y%3D%2218%22%3Ex%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1d8b8eed422c106ae9d7c55579f%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22104.5%22%20y%3D%2218%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22127.5%22%20y%3D%2218%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20text-anchor%3D%22middle%22%20x%3D%22141.5%22%20y%3D%2223%22%3E9%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22158.5%22%20y%3D%2218%22%3E20%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%229.5%22%20y%3D%2249%22%3E15%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1d8b8eed422c106ae9d7c55579f%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2230.5%22%20y%3D%2249%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2247.5%22%20y%3D%2249%22%3E4%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20text-anchor%3D%22middle%22%20x%3D%2255.5%22%20y%3D%2242%22%3E2%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2262.5%22%20y%3D%2242%22%3Ex%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1d8b8eed422c106ae9d7c55579f%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2278.5%22%20y%3D%2249%22%3E%26%23x21D4%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2294.5%22%20y%3D%2249%22%3E2%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22103.5%22%20y%3D%2249%22%3Ex%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1d8b8eed422c106ae9d7c55579f%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22120.5%22%20y%3D%2249%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22143.5%22%20y%3D%2249%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20text-anchor%3D%22middle%22%20x%3D%22157.5%22%20y%3D%2254%22%3E4%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22174.5%22%20y%3D%2249%22%3E15%3C%2Ftext%3E%3C%2Fsvg%3E)
Cas particulier :
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%224.5%22%20y%3D%2218%22%3En%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1d8b8eed422c106ae9d7c55579f%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2222.5%22%20y%3D%2218%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2245.5%22%20y%3D%2218%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2266.5%22%20y%3D%2218%22%3Em%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1d8b8eed422c106ae9d7c55579f%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2290.5%22%20y%3D%2218%22%3E%26%23x21D4%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22111.5%22%20y%3D%2218%22%3E10%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22123.5%22%20y%3D%2211%22%3En%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1d8b8eed422c106ae9d7c55579f%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22140.5%22%20y%3D%2218%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22159.5%22%20y%3D%2218%22%3Em%3C%2Ftext%3E%3C%2Fsvg%3E) "
Deuxième équivalence
Cette équivalence permet de calculer le logarithmique d'un nombre peut importe la base.
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'math192adcc127bfff5dc15e083854e'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAAExjdnQgDVUNBwAAAWgAAAA6Z2x5ZoPi2VsAAAGkAAABvmhlYWQQC2qxAAADZAAAADZoaGVhCGsXSAAAA5wAAAAkaG10eE2rRkcAAAPAAAAAFGxvY2EAHTwYAAAD1AAAABhtYXhwBT0FPgAAA%2BwAAAAgbmFtZaBxlY4AAAQMAAABn3Bvc3QB9wD6AAAFrAAAACBwcmVwa1uragAABcwAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEADgAAAAKAAgAAgACACwALgA9ImD%2F%2FwAAACwALgA9ImD%2F%2F%2F%2FV%2F9T%2Fxt2kAAEAAAAAAAAAAAAAAAABVAMsAIABAABWACoCWAIeAQ4BLAIsAFoBgAKAAKAA1ACAAAAAAAAAACsAVQCAAKsA1QEAASsABwAAAAIAVQAAAwADqwADAAcAADMRIRElIREhVQKr%2FasCAP4AA6v8VVUDAAABAFX%2FZADVAIAACgAAMzUzFRQGByc%2BATdVgC8vGx4eAYB6PVEUKQ40MQABACAAAACgAIAAAwAvGAGwBBCwA9SwAxCwAtSwAxCwADywAhCwATwAsAQQsAPUsAMQsAI8sAAQsAE8MDE3MxUjIICAgIAAAgCAAOsC1QIVAAMABwBlGAGwCBCwBtSwBhCwBdSwCBCwAdSwARCwANSwBhCwBzywBRCwBDywARCwAjywABCwAzwAsAgQsAbUsAYQsAfUsAcQsAHUsAEQsALUsAYQsAU8sAcQsAQ8sAEQsAA8sAIQsAM8MTATITUhHQEhNYACVf2rAlUBwFXVVVUAAwCAAHMC1QKPAAMABwALAGUYAbAMELAG1LAGELAF1LAMELAB1LABELAA1LAGELAHPLAFELAEPLABELACPLAAELADPACwDBCwBtSwBhCwB9SwBxCwAdSwARCwAtSwBhCwBTywBxCwBDywARCwADywAhCwAzwxMBMhNSEdASE1AwEzAYACVf2rAlV%2F%2FlZVAasBwFXVVVUBT%2F3kAhwAAAABAAAAAQAA1XjOQV8PPPUAAwQA%2F%2F%2F%2F%2F9Y6E3P%2F%2F%2F%2F%2F1joTcwAA%2FyAEgAOrAAAACgACAAEAAAAAAAEAAAPo%2F2oAABdwAAD%2FtgSAAAEAAAAAAAAAAAAAAAAAAAAFA1IAVQEzAFUAyAAgA1YAgANWAIAAAAAAAAAAKAAAAFIAAACYAAABIgAAAb4AAQAAAAUAXgAFAAAAAAACAIAEAAAAAAAEAADeAAAAAAAAABUBAgAAAAAAAAABABIAAAAAAAAAAAACAA4AEgAAAAAAAAADADAAIAAAAAAAAAAEABIAUAAAAAAAAAAFABYAYgAAAAAAAAAGAAkAeAAAAAAAAAAIABwAgQABAAAAAAABABIAAAABAAAAAAACAA4AEgABAAAAAAADADAAIAABAAAAAAAEABIAUAABAAAAAAAFABYAYgABAAAAAAAGAAkAeAABAAAAAAAIABwAgQADAAEECQABABIAAAADAAEECQACAA4AEgADAAEECQADADAAIAADAAEECQAEABIAUAADAAEECQAFABYAYgADAAEECQAGAAkAeAADAAEECQAIABwAgQBNAGEAdABoACAARgBvAG4AdABSAGUAZwB1AGwAYQByAE0AYQB0AGgAcwAgAEYAbwByACAATQBvAHIAZQAgAE0AYQB0AGgAIABGAG8AbgB0AE0AYQB0AGgAIABGAG8AbgB0AFYAZQByAHMAaQBvAG4AIAAxAC4AME1hdGhfRm9udABNAGEAdABoAHMAIABGAG8AcgAgAE0AbwByAGUAAAMAAAAAAAAB9AD6AAAAAAAAAAAAAAAAAAAAAAAAAAC5BxEAAI2FGACyAAAAFRQTsQABPw%3D%3D)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%2217.5%22%20y%3D%2248%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2219%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2240.5%22%20y%3D%2255%22%3Ec%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2264.5%22%20y%3D%2248%22%3Em%3C%2Ftext%3E%3Ctext%20font-family%3D%22math192adcc127bfff5dc15e083854e%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%2298.5%22%20y%3D%2248%22%3E%3D%3C%2Ftext%3E%3Cline%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%22115.5%22%20x2%3D%22191.5%22%20y1%3D%2238.5%22%20y2%3D%2238.5%22%2F%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22135.5%22%20y%3D%2224%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2219%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22158.5%22%20y%3D%2231%22%3Ed%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22176.5%22%20y%3D%2224%22%3Em%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22125.5%22%20y%3D%2265%22%3El%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22135.5%22%20y%3D%2265%22%3Eo%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22149.5%22%20y%3D%2265%22%3Eg%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2219%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22163.5%22%20y%3D%2272%22%3Ed%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22176.5%22%20y%3D%2265%22%3Ec%3C%2Ftext%3E%3Ctext%20font-family%3D%22math192adcc127bfff5dc15e083854e%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22206.5%22%20y%3D%2248%22%3E%2C%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22224.5%22%20y%3D%2248%22%3Eo%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22238.5%22%20y%3D%2248%22%3E%26%23xF9%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22265.5%22%20y%3D%2248%22%3Em%3C%2Ftext%3E%3Ctext%20font-family%3D%22math192adcc127bfff5dc15e083854e%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22292.5%22%20y%3D%2248%22%3E%26%23x2260%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22313.5%22%20y%3D%2248%22%3E0%3C%2Ftext%3E%3Ctext%20font-family%3D%22math192adcc127bfff5dc15e083854e%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22324.5%22%20y%3D%2248%22%3E%2C%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22341.5%22%20y%3D%2248%22%3Ec%3C%2Ftext%3E%3Ctext%20font-family%3D%22math192adcc127bfff5dc15e083854e%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22364.5%22%20y%3D%2248%22%3E%26%23x2260%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22385.5%22%20y%3D%2248%22%3E0%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22406.5%22%20y%3D%2248%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22416.5%22%20y%3D%2248%22%3Et%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22436.5%22%20y%3D%2248%22%3Eo%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22450.5%22%20y%3D%2248%22%3Eu%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22469.5%22%20y%3D%2248%22%3El%3C%2Ftext%3E%3Ctext%20font-family%3D%22a5b0e8edda16aced741108dbc8eca69%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22479.5%22%20y%3D%2248%22%3Ea%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22502.5%22%20y%3D%2248%22%3Eb%3C%2Ftext%3E%3Ctext%20font-family%3D%22a5b0e8edda16aced741108dbc8eca69%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22516.5%22%20y%3D%2248%22%3Ea%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22529.5%22%20y%3D%2248%22%3Es%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22543.5%22%20y%3D%2248%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22566.5%22%20y%3D%2248%22%3Ed%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22589.5%22%20y%3D%2248%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22602.5%22%20y%3D%2248%22%3Es%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22612.5%22%20y%3D%2248%22%3Et%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22631.5%22%20y%3D%2248%22%3Es%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22645.5%22%20y%3D%2248%22%3Eu%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22659.5%22%20y%3D%2248%22%3Ep%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22673.5%22%20y%3D%2248%22%3E%26%23xE9%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22684.5%22%20y%3D%2248%22%3Er%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22692.5%22%20y%3D%2248%22%3Ei%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22702.5%22%20y%3D%2248%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22716.5%22%20y%3D%2248%22%3Eu%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22727.5%22%20y%3D%2248%22%3Er%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22739.5%22%20y%3D%2248%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22762.5%22%20y%3D%2248%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22772.5%22%20y%3D%2248%22%3Et%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22792.5%22%20y%3D%2248%22%3Ed%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22802.5%22%20y%3D%2248%22%3Ei%3C%2Ftext%3E%3Ctext%20font-family%3D%22a5b0e8edda16aced741108dbc8eca69%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22810.5%22%20y%3D%2248%22%3Ef%3C%2Ftext%3E%3Ctext%20font-family%3D%22a5b0e8edda16aced741108dbc8eca69%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22823.5%22%20y%3D%2248%22%3Ef%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22838.5%22%20y%3D%2248%22%3E%26%23xE9%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22849.5%22%20y%3D%2248%22%3Er%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22861.5%22%20y%3D%2248%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22875.5%22%20y%3D%2248%22%3En%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22885.5%22%20y%3D%2248%22%3Et%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22896.5%22%20y%3D%2248%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22919.5%22%20y%3D%2248%22%3Ed%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22933.5%22%20y%3D%2248%22%3Ee%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22956.5%22%20y%3D%2248%22%3E1%3C%2Ftext%3E%3Ctext%20font-family%3D%22math192adcc127bfff5dc15e083854e%22%20font-size%3D%2226%22%20text-anchor%3D%22middle%22%20x%3D%22967.5%22%20y%3D%2248%22%3E.%3C%2Ftext%3E%3C%2Fsvg%3E)
Exemples
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'brack_sm2882ad605b1e27be87c7468'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7PH4UAAADMAAAATmNtYXA3kjw6AAABHAAAADxjdnQgAQYDiAAAAVgAAAASZ2x5ZkyYQ7YAAAFsAAAAkWhlYWQLyR8fAAACAAAAADZoaGVhAq0XCAAAAjgAAAAkaG10eDEjA%2FUAAAJcAAAADGxvY2EAAEKZAAACaAAAABBtYXhwBJsEcQAAAngAAAAgbmFtZW7QvZAAAAKYAAAB5XBvc3QArQBVAAAEgAAAACBwcmVwu5WEAAAABKAAAAAHAAACDAGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg9AMD%2FP%2F8AAABVAABAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACI5wjn%2F%2F%2FAAAjnCOf%2F%2F%2FcZdxjAAEAAAAAAAAAAAFUAFQBAAArAIwAgACoAAcAAAACAAAAAADVAQEAAwAHAAAxMxEjFyM1M9XVq4CAAQHWqwABAAAAAABVAVgAAwAfGAGwAy%2BwADyxAgL1sAE8ALEDAD%2BwAjx8sQAG9bABPBEzESNVVQFY%2FqgAAQDXAAABLAFUAAMAIBgBsAUvsAE8sAI8sQAC9bADPACwAy%2BwAjyxAAH1sAE8EzMRI9dVVQFU%2FqwAAAAAAQAAAAEAAIsesexfDzz1AAMEAP%2F%2F%2F%2F%2FVre5k%2F%2F%2F%2F%2F9Wt7mT%2FgP%2F%2FAdYBWAAAAAoAAgABAAAAAAABAAABVP%2F%2FAAAXcP%2BA%2F4AB1gABAAAAAAAAAAAAAAAAAAAAAwDVAAABLAAAASwA1wAAAAAAAAAhAAAAWAAAAJEAAQAAAAMACgACAAAAAAACAIAEAAAAAAAEAABlAAAAAAAAABUBAgAAAAAAAAABACYAAAAAAAAAAAACAA4AJgAAAAAAAAADAEQANAAAAAAAAAAEACYAeAAAAAAAAAAFABYAngAAAAAAAAAGABMAtAAAAAAAAAAIABwAxwABAAAAAAABACYAAAABAAAAAAACAA4AJgABAAAAAAADAEQANAABAAAAAAAEACYAeAABAAAAAAAFABYAngABAAAAAAAGABMAtAABAAAAAAAIABwAxwADAAEECQABACYAAAADAAEECQACAA4AJgADAAEECQADAEQANAADAAEECQAEACYAeAADAAEECQAFABYAngADAAEECQAGABMAtAADAAEECQAIABwAxwBCAHIAYQBjAGsAZQB0AHMAIABzAG0AYQBsAGwAIABzAGkAegBlAFIAZQBnAHUAbABhAHIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlACAAQgByAGEAYwBrAGUAdABzACAAcwBtAGEAbABsACAAcwBpAHoAZQBCAHIAYQBjAGsAZQB0AHMAIABzAG0AYQBsAGwAIABzAGkAegBlAFYAZQByAHMAaQBvAG4AIAAyAC4AMEJyYWNrZXRzX3NtYWxsX3NpemUATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlAAAAAAMAAAAAAAAAqgBVAAAAAAAAAAAAAAAAAAAAAAAAAAC5B%2F8AAo2FAA%3D%3D)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'bracketse552f5417ff4680c6b50499'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7RIisAAADMAAAATmNtYXBi7uzYAAABHAAAAExjdnQgBAkDLgAAAWgAAAASZ2x5Zo64f%2BkAAAF8AAABSWhlYWQLniGcAAACyAAAADZoaGVhBK4XLAAAAwAAAAAkaG10eCWq%2F90AAAMkAAAAFGxvY2EAABknAAADOAAAABhtYXhwBJIESAAAA1AAAAAgbmFtZRAA8I4AAANwAAAB3nBvc3QBwwDgAAAFUAAAACBwcmVwupWEAAAABXAAAAAHAAACggGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg9AMEAAAAAAADgAAAAAAAAAACAAEAAQAAABQAAwABAAAAFAAEADgAAAAKAAgAAgACI5sjnSOeI6D%2F%2FwAAI5sjnSOeI6D%2F%2F9xm3GXcZdxkAAEAAAAAAAAAAAAAAAABVABWAQAALACoA4AAMgAHAAAAAgAAACoA1QNVAAMABwAANTMRIxMjETPV1auAgCoDK%2F0AAtUAAQAAAAABgAOAAAUAJBgBsAAvsAPFsQEC%2FbADELEEBP0AsQAAP7ABPLEEBj%2BwAzwwMTEzEAEjAFUBKyv%2BqwH8AYT%2BqgABAAAAAAGAA4AABQAmGAGwAC6wA8WxBQL9sAMQsQIE%2FQB8sQAGPxiwBTyxAwb2sAI8MDEREgEzABMBAVQr%2FtMCA4D91v6qAYQB%2FAAB%2F6wAAAEsA4AABQAnGAGwAC%2BwBzywA8WxAQL9sAMQsQQE%2FQCxAAA%2FsAE8sQQGP7ADPDAxISMSATMAASxVAf7UKwFVAfwBhP6rAAH%2FrAAAASwDgAAFACkYAbABL7AHPLAExbEAAv2wBBCxAwT9AHyxAQY%2FsAA8GLEEAD%2BwAzwwMRMzEAEjANdV%2FqsrASsDgP3V%2FqsBhgAAAAABAAAAAQAAeuTcpl8PPPUAAwQA%2F%2F%2F%2F%2F9Wt7o7%2F%2F%2F%2F%2F1a3ujv%2BsAAABgAOAAAAACgACAAEAAAAAAAEAAAOAAAAAABdw%2F6z%2FrAGAAAEAAAAAAAAAAAAAAAAAAAAFANUAAAEsAAABLAAAASz%2FrAEs%2F6wAAAAAAAAAJAAAAGgAAACzAAAA%2FQAAAUkAAQAAAAUACAACAAAAAAACAIAEAAAAAAAEAAA%2BAAAAAAAAABUBAgAAAAAAAAABACQAAAAAAAAAAAACAA4AJAAAAAAAAAADAEIAMgAAAAAAAAAEACQAdAAAAAAAAAAFABYAmAAAAAAAAAAGABIArgAAAAAAAAAIABwAwAABAAAAAAABACQAAAABAAAAAAACAA4AJAABAAAAAAADAEIAMgABAAAAAAAEACQAdAABAAAAAAAFABYAmAABAAAAAAAGABIArgABAAAAAAAIABwAwAADAAEECQABACQAAAADAAEECQACAA4AJAADAAEECQADAEIAMgADAAEECQAEACQAdAADAAEECQAFABYAmAADAAEECQAGABIArgADAAEECQAIABwAwABCAHIAYQBjAGsAZQB0AHMAIABmAHUAbABsACAAcwBpAHoAZQBSAGUAZwB1AGwAYQByAE0AYQB0AGgAcwAgAEYAbwByACAATQBvAHIAZQAgAEIAcgBhAGMAawBlAHQAcwAgAGYAdQBsAGwAIABzAGkAegBlAEIAcgBhAGMAawBlAHQAcwAgAGYAdQBsAGwAIABzAGkAegBlAFYAZQByAHMAaQBvAG4AIAAyAC4AMEJyYWNrZXRzX2Z1bGxfc2l6ZQBNAGEAdABoAHMAIABGAG8AcgAgAE0AbwByAGUAAAADAAAAAAAAAcAA4AAAAAAAAAAAAAAAAAAAAAAAAAAAuQf%2FAAGNhQA%3D)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2210.5%22%20y%3D%2227%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20text-anchor%3D%22middle%22%20x%3D%2224.5%22%20y%3D%2232%22%3E2%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2232.5%22%20y%3D%2227%22%3E7%3C%2Ftext%3E%3Ctext%20font-family%3D%22math17f39f8317fbdb1988ef4c628eb%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2249.5%22%20y%3D%2227%22%3E%3D%3C%2Ftext%3E%3Cline%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%2260.5%22%20x2%3D%2297.5%22%20y1%3D%2221.5%22%20y2%3D%2221.5%22%2F%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2272.5%22%20y%3D%2216%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2291.5%22%20y%3D%2216%22%3E7%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2272.5%22%20y%3D%2239%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2291.5%22%20y%3D%2239%22%3E2%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%224.5%22%20y%3D%2274%22%3E4%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2223.5%22%20y%3D%2274%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20text-anchor%3D%22middle%22%20x%3D%2237.5%22%20y%3D%2279%22%3E5%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2245.5%22%20y%3D%2274%22%3E9%3C%2Ftext%3E%3Ctext%20font-family%3D%22math17f39f8317fbdb1988ef4c628eb%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2262.5%22%20y%3D%2274%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2279.5%22%20y%3D%2274%22%3E4%3C%2Ftext%3E%3Ctext%20font-family%3D%22bracketse552f5417ff4680c6b50499%22%20font-size%3D%2216%22%20text-anchor%3D%22start%22%20x%3D%2285.5%22%20y%3D%2264%22%3E%26%23x239B%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22brack_sm2882ad605b1e27be87c7468%22%20font-size%3D%2216%22%20text-anchor%3D%22start%22%20x%3D%2285.5%22%20y%3D%2269%22%3E%26%23x239C%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22brack_sm2882ad605b1e27be87c7468%22%20font-size%3D%2216%22%20text-anchor%3D%22start%22%20x%3D%2285.5%22%20y%3D%2274%22%3E%26%23x239C%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22bracketse552f5417ff4680c6b50499%22%20font-size%3D%2216%22%20text-anchor%3D%22start%22%20x%3D%2285.5%22%20y%3D%2288%22%3E%26%23x239D%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22bracketse552f5417ff4680c6b50499%22%20font-size%3D%2216%22%20text-anchor%3D%22start%22%20x%3D%22134.5%22%20y%3D%2264%22%3E%26%23x239E%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22brack_sm2882ad605b1e27be87c7468%22%20font-size%3D%2216%22%20text-anchor%3D%22start%22%20x%3D%22134.5%22%20y%3D%2269%22%3E%26%23x239F%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22brack_sm2882ad605b1e27be87c7468%22%20font-size%3D%2216%22%20text-anchor%3D%22start%22%20x%3D%22134.5%22%20y%3D%2274%22%3E%26%23x239F%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22bracketse552f5417ff4680c6b50499%22%20font-size%3D%2216%22%20text-anchor%3D%22start%22%20x%3D%22134.5%22%20y%3D%2288%22%3E%26%23x23A0%3B%3C%2Ftext%3E%3Cline%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%2293.5%22%20x2%3D%22130.5%22%20y1%3D%2268.5%22%20y2%3D%2268.5%22%2F%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22105.5%22%20y%3D%2263%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22124.5%22%20y%3D%2263%22%3E9%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22105.5%22%20y%3D%2286%22%3Elog%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22124.5%22%20y%3D%2286%22%3E5%3C%2Ftext%3E%3C%2Fsvg%3E)
Écoute les 10 premières minutes de la vidéo.
|
|
 Recherche de la règle d'une fonction logarithmique Recherche de la règle d'une fonction logarithmique |
|
|
 Vidéo de théorie et exercices-Fonctions périodique et définie par parties Vidéo de théorie et exercices-Fonctions périodique et définie par parties |
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Fonction racine carrée Fonction racine carrée |
Les radicaux
Par convention, on écrit 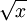 ou ou ![\sqrt[2] {x}](http://recit.csbe.qc.ca/fel/math/math_img/c5b6de7f8df033feedb4ac12485487f2.png) pour exprimer la racine carrée de x. pour exprimer la racine carrée de x.
La racine carrée est un exposant fractionnaire de ½ .
En effet, ![\sqrt 4 = 4^{\frac {1}{2}}= \sqrt[2] {4}](http://recit.csbe.qc.ca/fel/math/math_img/3ef93790424ccf92118232b3fff32409.png) ![= \sqrt[2] {2^2} = 2](http://recit.csbe.qc.ca/fel/math/math_img/9c38f654408d076bb1338b3354aef82c.png) . .
De la même façon :
Ou encore :
Propriétés des radicaux
|
Propriétés
|
Restrictions
|
Exemples
|
|
, |
|
|
|
|
|
|
|
|
|
|
Théorie

La fonction racine carrée
La fonction racine carrée de base s'exprime à l'aide de la règle : 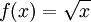 . .
La représentation graphique est une courbe dont le sommet est à l'origine du plan cartésien.
En lui appliquant les paramètres multiplicatifs a et b, on obtient :
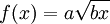 où a et b sont différents de zéro.
Voici le graphique de la fonction racine carrée transformée:
Utilise les curseurs a et b pour voir les modifications de la courbe.
Recherche de la règle d'une fonction racine carrée
Dans les préalables, tu as étudié les propriétés des radicaux. Ils nous permettent de transformer une règle de la forme
en une règle de la forme 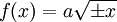
Exemples
Pour déterminer la règle d'une fonction racine carrée dont la règle est de forme
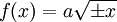 , il faut : , il faut :
1 - Déduire la forme de la règle, soit
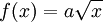 , si l'ouverture est vers la droite.
ou 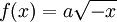 , si l'ouverture est vers la gauche.
2 - Trouver les coordonnées d'un point de la courbe autre que le sommet;
3 - Remplacer les coordonnées de ce point dans la règle;
4 - Résoudre l'équation obtenue afin de trouver la valeur du paramètre a;
5 - Écrire la règle de la fonction obtenue.
|
|
 Rôle du paramètre a dans la fonction f(x)=ax² Rôle du paramètre a dans la fonction f(x)=ax² |
Rôle du paramètre a dans la fonction f(x)=ax² |
|
 Rôle du paramètre a dans la fonction exponentielle f(x)=a(c)^x Rôle du paramètre a dans la fonction exponentielle f(x)=a(c)^x |
|
|
 Exercices de révision du chapitre 2 Exercices de révision du chapitre 2 |
Exercices de révision du chapitre 2 |
|
| Chapitre 3 |
 Résumé des notes de cours chap2 Résumé des notes de cours chap2 |
Résumé des notes de cours chap. 2 |
|
 Droite y = ax + b Droite y = ax + b |
|
|
| Chapitre 4 |
 Résumé des notes de cours chap4 Résumé des notes de cours chap4 |
|
|
 Vidéo de théorie et exercices-Triangles isométriques Vidéo de théorie et exercices-Triangles isométriques |
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Vidéo de théorie et exercices-Triangles semblables Vidéo de théorie et exercices-Triangles semblables |
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Vidéo de théorie et exercices-Triangles rectangles (rapports trigonométriques) Vidéo de théorie et exercices-Triangles rectangles (rapports trigonométriques) |
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Vidéo de théorie et exercices-Relations métriques dans le triangle rectangle Vidéo de théorie et exercices-Relations métriques dans le triangle rectangle |
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Vidéo de théorie et exercices-Loi des sinus Vidéo de théorie et exercices-Loi des sinus |
|
1- Écouter la vidéo ci-dessous.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Vidéo de théorie et exercices-Loi des cosinus Vidéo de théorie et exercices-Loi des cosinus |
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Vidéo de théorie-Formule de Héron Vidéo de théorie-Formule de Héron |
| Cette petite partie est optionnelle mais il est fortement suggéré de l'écouter. La formule de Héron est un outil très intéressant pour trouver l'aire d'un triangle à partir des mesures de ses trois côtés. Tu peux l'utiliser au besoin. |
|
|
|
 Vidéo de théorie et exercices-Les figures équivalentes Vidéo de théorie et exercices-Les figures équivalentes |
|
1- Écouter la vidéo ci-dessous.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Exercices de révision du chapitre 4 Exercices de révision du chapitre 4 |
Exercices de révision du chapitre 4 |
|
| Chapitre 5 |
 Résumé des notes de cours chapitre 5 Résumé des notes de cours chapitre 5 |
Résumé des notes de cours chapitre 5 |
|
 Vidéo de théorie et exercices-Tableau à double entrée et nuage de points Vidéo de théorie et exercices-Tableau à double entrée et nuage de points |
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Vidéo de théorie et exercices-Coefficient de corrélation Vidéo de théorie et exercices-Coefficient de corrélation |
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Intensité du coefficient de corrélation Intensité du coefficient de corrélation |
|
|
 Vidéo de théorie et exercices-La droite de régression Vidéo de théorie et exercices-La droite de régression |
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Droite de régression Droite de régression |
|
|
 Vidéo de théorie et exercices-Écart moyen Vidéo de théorie et exercices-Écart moyen |
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
 Écart type Écart type |
L'écart type est une mesure qui caractérise la dispersion des données d'une distribution.
Pour trouver l'écart type d'une distribution, il faut:
1) Trouver la moyenne de la distribution.
2) Calculer le carré de l'écart des données à la moyenne.
3) Faire la somme des carrés des écarts à la moyenne.
4) Calculer le nombre total de données de la distribution.
5) Remplacer ces valeurs dans la formule suivantes:
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'math17f39f8317fbdb1988ef4c628eb'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAADRjdnQgDVUNBwAAAVAAAAA6Z2x5ZoPi2VsAAAGMAAAAsmhlYWQQC2qxAAACQAAAADZoaGVhCGsXSAAAAngAAAAkaG10eE2rRkcAAAKcAAAACGxvY2EAHTwYAAACpAAAAAxtYXhwBT0FPgAAArAAAAAgbmFtZaBxlY4AAALQAAABn3Bvc3QB9wD6AAAEcAAAACBwcmVwa1uragAABJAAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACAAAAAEAAQAAQAAAD3%2F%2FwAAAD3%2F%2F%2F%2FEAAEAAAAAAAABVAMsAIABAABWACoCWAIeAQ4BLAIsAFoBgAKAAKAA1ACAAAAAAAAAACsAVQCAAKsA1QEAASsABwAAAAIAVQAAAwADqwADAAcAADMRIRElIREhVQKr%2FasCAP4AA6v8VVUDAAACAIAA6wLVAhUAAwAHAGUYAbAIELAG1LAGELAF1LAIELAB1LABELAA1LAGELAHPLAFELAEPLABELACPLAAELADPACwCBCwBtSwBhCwB9SwBxCwAdSwARCwAtSwBhCwBTywBxCwBDywARCwADywAhCwAzwxMBMhNSEdASE1gAJV%2FasCVQHAVdVVVQAAAAEAAAABAADVeM5BXw889QADBAD%2F%2F%2F%2F%2F1joTc%2F%2F%2F%2F%2F%2FWOhNzAAD%2FIASAA6sAAAAKAAIAAQAAAAAAAQAAA%2Bj%2FagAAF3AAAP%2B2BIAAAQAAAAAAAAAAAAAAAAAAAAIDUgBVA1YAgAAAAAAAAAAoAAAAsgABAAAAAgBeAAUAAAAAAAIAgAQAAAAAAAQAAN4AAAAAAAAAFQECAAAAAAAAAAEAEgAAAAAAAAAAAAIADgASAAAAAAAAAAMAMAAgAAAAAAAAAAQAEgBQAAAAAAAAAAUAFgBiAAAAAAAAAAYACQB4AAAAAAAAAAgAHACBAAEAAAAAAAEAEgAAAAEAAAAAAAIADgASAAEAAAAAAAMAMAAgAAEAAAAAAAQAEgBQAAEAAAAAAAUAFgBiAAEAAAAAAAYACQB4AAEAAAAAAAgAHACBAAMAAQQJAAEAEgAAAAMAAQQJAAIADgASAAMAAQQJAAMAMAAgAAMAAQQJAAQAEgBQAAMAAQQJAAUAFgBiAAMAAQQJAAYACQB4AAMAAQQJAAgAHACBAE0AYQB0AGgAIABGAG8AbgB0AFIAZQBnAHUAbABhAHIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlACAATQBhAHQAaAAgAEYAbwBuAHQATQBhAHQAaAAgAEYAbwBuAHQAVgBlAHIAcwBpAG8AbgAgADEALgAwTWF0aF9Gb250AE0AYQB0AGgAcwAgAEYAbwByACAATQBvAHIAZQAAAwAAAAAAAAH0APoAAAAAAAAAAAAAAAAAAAAAAAAAALkHEQAAjYUYALIAAAAVFBOxAAE%2F)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%225.5%22%20y%3D%2235%22%3E%26%23xE9%3B%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2214.5%22%20y%3D%2235%22%3Ec%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22ae2ef524fbf3d9fe611d5a8e90fefdc%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2224.5%22%20y%3D%2235%22%3Ea%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2232.5%22%20y%3D%2235%22%3Er%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2237.5%22%20y%3D%2235%22%3Et%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2248.5%22%20y%3D%2235%22%3Et%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2255.5%22%20y%3D%2235%22%3Ey%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2265.5%22%20y%3D%2235%22%3Ep%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2275.5%22%20y%3D%2235%22%3Ee%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22math17f39f8317fbdb1988ef4c628eb%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2290.5%22%20y%3D%2235%22%3E%3D%3C%2Ftext%3E%3Cpolyline%20fill%3D%22none%22%20points%3D%2214%2C-47%2013%2C-47%206%2C0%202%2C-19%22%20stroke%3D%22%230000FF%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20transform%3D%22translate(105.5%2C50.5)%22%2F%3E%3Cpolyline%20fill%3D%22none%22%20points%3D%226%2C0%202%2C-19%201%2C-16%22%20stroke%3D%22%230000FF%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20transform%3D%22translate(105.5%2C50.5)%22%2F%3E%3Cline%20stroke%3D%22%230000FF%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%22119.5%22%20x2%3D%22487.5%22%20y1%3D%223.5%22%20y2%3D%223.5%22%2F%3E%3Cline%20stroke%3D%22%230000FF%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%22123.5%22%20x2%3D%22483.5%22%20y1%3D%2228.5%22%20y2%3D%2228.5%22%2F%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22129.5%22%20y%3D%2222%22%3Es%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22139.5%22%20y%3D%2222%22%3Eo%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22151.5%22%20y%3D%2222%22%3Em%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22166.5%22%20y%3D%2222%22%3Em%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22179.5%22%20y%3D%2222%22%3Ee%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22195.5%22%20y%3D%2222%22%3Ed%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22205.5%22%20y%3D%2222%22%3Ee%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22214.5%22%20y%3D%2222%22%3Es%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22229.5%22%20y%3D%2222%22%3Ec%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22ae2ef524fbf3d9fe611d5a8e90fefdc%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22239.5%22%20y%3D%2222%22%3Ea%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22247.5%22%20y%3D%2222%22%3Er%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22253.5%22%20y%3D%2222%22%3Er%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22261.5%22%20y%3D%2222%22%3E%26%23xE9%3B%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22270.5%22%20y%3D%2222%22%3Es%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22286.5%22%20y%3D%2222%22%3Ed%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22296.5%22%20y%3D%2222%22%3Ee%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22305.5%22%20y%3D%2222%22%3Es%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22321.5%22%20y%3D%2222%22%3E%26%23xE9%3B%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22330.5%22%20y%3D%2222%22%3Ec%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22ae2ef524fbf3d9fe611d5a8e90fefdc%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22340.5%22%20y%3D%2222%22%3Ea%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22348.5%22%20y%3D%2222%22%3Er%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22353.5%22%20y%3D%2222%22%3Et%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22360.5%22%20y%3D%2222%22%3Es%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22376.5%22%20y%3D%2222%22%3E%26%23xE0%3B%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22389.5%22%20y%3D%2222%22%3El%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22ae2ef524fbf3d9fe611d5a8e90fefdc%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22396.5%22%20y%3D%2222%22%3Ea%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22414.5%22%20y%3D%2222%22%3Em%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22427.5%22%20y%3D%2222%22%3Eo%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22436.5%22%20y%3D%2222%22%3Ey%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22446.5%22%20y%3D%2222%22%3Ee%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22456.5%22%20y%3D%2222%22%3En%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22466.5%22%20y%3D%2222%22%3En%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22476.5%22%20y%3D%2222%22%3Ee%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22207.5%22%20y%3D%2248%22%3En%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22217.5%22%20y%3D%2248%22%3Eo%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22229.5%22%20y%3D%2248%22%3Em%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22242.5%22%20y%3D%2248%22%3Eb%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22250.5%22%20y%3D%2248%22%3Er%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22258.5%22%20y%3D%2248%22%3Ee%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22271.5%22%20y%3D%2248%22%3Et%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22279.5%22%20y%3D%2248%22%3Eo%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22286.5%22%20y%3D%2248%22%3Et%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22ae2ef524fbf3d9fe611d5a8e90fefdc%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22294.5%22%20y%3D%2248%22%3Ea%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22301.5%22%20y%3D%2248%22%3El%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22314.5%22%20y%3D%2248%22%3Ed%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22324.5%22%20y%3D%2248%22%3Ee%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22340.5%22%20y%3D%2248%22%3Ed%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22350.5%22%20y%3D%2248%22%3Eo%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22360.5%22%20y%3D%2248%22%3En%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22370.5%22%20y%3D%2248%22%3En%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22380.5%22%20y%3D%2248%22%3E%26%23xE9%3B%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22390.5%22%20y%3D%2248%22%3Ee%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22399.5%22%20y%3D%2248%22%3Es%3C%2Ftext%3E%3C%2Fsvg%3E)
Selon la situation :
-
- un écart type considéré comme petit signifie que les données sont concentrées de chaque côté de la moyenne.
- un écart type considéré comme grand signifie que les données sont dispersées de chaque côté de la moyenne.
On peut facilement imaginer que le calcul de l'écart-type est fastidieux. C'est pourquoi, le plus souvent, on l'effectue à l'aide de la calculatrice ou un moyen technologique équivalent.
|
|
 Exercices de révision du chapitre 5 Exercices de révision du chapitre 5 |
Exercices de révision du chapitre 5 |
|
| Chapitre 6 |
 Résumé des notes de cours Chapitre 6 Résumé des notes de cours Chapitre 6 |
Résumé des notes de cours Chapitre 6 |
|
 Vidéo de théorie et exercices -Types de probabilités Vidéo de théorie et exercices -Types de probabilités |
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
|
|
 Probabilité conditionnelle Probabilité conditionnelle |
Probabilité conditionnelle
La probabilité qu'un événement se réalise sachant qu'un autre événement se réalise ou étant donné qu'un autre événement s'est déjà réalisé se nomme probabilité conditionnelle.
Probabilité de B étant donné A =
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'round_brackets18549f92a457f2409'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMjwHLFQAAADMAAAATmNtYXDf7xCrAAABHAAAADxjdnQgBAkDLgAAAVgAAAASZ2x5ZmAOz2cAAAFsAAABJGhlYWQOKih8AAACkAAAADZoaGVhCvgVwgAAAsgAAAAkaG10eCA6AAIAAALsAAAADGxvY2EAAARLAAAC%2BAAAABBtYXhwBIgEWQAAAwgAAAAgbmFtZXHR30MAAAMoAAACOXBvc3QDogHPAAAFZAAAACBwcmVwupWEAAAABYQAAAAHAAAGcgGQAAUAAAgACAAAAAAACAAIAAAAAAAAAQIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAo8AMGe%2F57AAAHPgGyAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACACgAKf%2F%2FAAAAKAAp%2F%2F%2F%2F2f%2FZAAEAAAAAAAAAAAFUAFYBAAAsAKgDgAAyAAcAAAACAAAAKgDVA1UAAwAHAAA1MxEjEyMRM9XVq4CAKgMr%2FQAC1QABAAD%2B0AIgBtAACQBNGAGwChCwA9SwAxCwAtSwChCwBdSwBRCwANSwAxCwBzywAhCwCDwAsAoQsAPUsAMQsAfUsAoQsAXUsAoQsADUsAMQsAI8sAcQsAg8MTAREAEzABEQASMAAZCQ%2FnABkJD%2BcALQ%2FZD%2BcAGQAnACcAGQ%2FnAAAQAA%2FtACIAbQAAkATRgBsAoQsAPUsAMQsALUsAoQsAXUsAUQsADUsAMQsAc8sAIQsAg8ALAKELAD1LADELAH1LAKELAF1LAKELAA1LADELACPLAHELAIPDEwARABIwAREAEzAAIg%2FnCQAZD%2BcJABkALQ%2FZD%2BcAGQAnACcAGQ%2FnAAAQAAAAEAAPW2NYFfDzz1AAMIAP%2F%2F%2F%2F%2FVre7u%2F%2F%2F%2F%2F9Wt7u4AAP7QA7cG0AAAAAoAAgABAAAAAAABAAAHPv5OAAAXcAAA%2F%2F4DtwABAAAAAAAAAAAAAAAAAAAAAwDVAAACIAAAAiAAAAAAAAAAAAAkAAAAowAAASQAAQAAAAMACgACAAAAAAACAIAEAAAAAAAEAABNAAAAAAAAABUBAgAAAAAAAAABAD4AAAAAAAAAAAACAA4APgAAAAAAAAADAFwATAAAAAAAAAAEAD4AqAAAAAAAAAAFABYA5gAAAAAAAAAGAB8A%2FAAAAAAAAAAIABwBGwABAAAAAAABAD4AAAABAAAAAAACAA4APgABAAAAAAADAFwATAABAAAAAAAEAD4AqAABAAAAAAAFABYA5gABAAAAAAAGAB8A%2FAABAAAAAAAIABwBGwADAAEECQABAD4AAAADAAEECQACAA4APgADAAEECQADAFwATAADAAEECQAEAD4AqAADAAEECQAFABYA5gADAAEECQAGAB8A%2FAADAAEECQAIABwBGwBSAG8AdQBuAGQAIABiAHIAYQBjAGsAZQB0AHMAIAB3AGkAdABoACAAYQBzAGMAZQBuAHQAIAAxADgANQA0AFIAZQBnAHUAbABhAHIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlACAAUgBvAHUAbgBkACAAYgByAGEAYwBrAGUAdABzACAAdwBpAHQAaAAgAGEAcwBjAGUAbgB0ACAAMQA4ADUANABSAG8AdQBuAGQAIABiAHIAYQBjAGsAZQB0AHMAIAB3AGkAdABoACAAYQBzAGMAZQBuAHQAIAAxADgANQA0AFYAZQByAHMAaQBvAG4AIAAyAC4AMFJvdW5kX2JyYWNrZXRzX3dpdGhfYXNjZW50XzE4NTQATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlAAAAAAMAAAAAAAADnwHPAAAAAAAAAAAAAAAAAAAAAAAAAAC5B%2F8AAY2FAA%3D%3D)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%225.5%22%20y%3D%2216%22%3EP%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2215.5%22%20y%3D%2216%22%3E(%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2250.5%22%20y%3D%2216%22%3E)%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2222.5%22%20y%3D%2216%22%3EB%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22math14a3a0e95f6f369046401c7b1c1%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2232.5%22%20y%3D%2216%22%3E%7C%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2241.5%22%20y%3D%2216%22%3EA%3C%2Ftext%3E%3Ctext%20fill%3D%22%2300007F%22%20font-family%3D%22math14a3a0e95f6f369046401c7b1c1%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2261.5%22%20y%3D%2216%22%3E%3D%3C%2Ftext%3E%3Cline%20stroke%3D%22%230000FF%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%222.5%22%20x2%3D%2266.5%22%20y1%3D%2245.5%22%20y2%3D%2245.5%22%2F%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%229.5%22%20y%3D%2240%22%3EP%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2219.5%22%20y%3D%2240%22%3E(%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2262.5%22%20y%3D%2240%22%3E)%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2226.5%22%20y%3D%2240%22%3EA%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22math14a3a0e95f6f369046401c7b1c1%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2240.5%22%20y%3D%2240%22%3E%26%23x2229%3B%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2253.5%22%20y%3D%2240%22%3EB%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2223.5%22%20y%3D%2262%22%3EP%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2233.5%22%20y%3D%2262%22%3E(%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2249.5%22%20y%3D%2262%22%3E)%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2240.5%22%20y%3D%2262%22%3EA%3C%2Ftext%3E%3Ctext%20fill%3D%22%2300007F%22%20font-family%3D%22math14a3a0e95f6f369046401c7b1c1%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2277.5%22%20y%3D%2251%22%3E%3D%3C%2Ftext%3E%3Ctext%20fill%3D%22%2300007F%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%224.5%22%20y%3D%2286%22%3Eo%3C%2Ftext%3E%3Ctext%20fill%3D%22%2300007F%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2213.5%22%20y%3D%2286%22%3E%26%23xF9%3B%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2228.5%22%20y%3D%2286%22%3EP%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2238.5%22%20y%3D%2286%22%3E(%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2254.5%22%20y%3D%2286%22%3E)%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2245.5%22%20y%3D%2286%22%3EA%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22math14a3a0e95f6f369046401c7b1c1%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2265.5%22%20y%3D%2286%22%3E%26%23x2260%3B%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2278.5%22%20y%3D%2286%22%3E0%3C%2Ftext%3E%3C%2Fsvg%3E)
Cette probabilité correspond à la probabilité de l'intersection de l'événement A et B sur la probabilité de l'événement A.
On peut noter cette probabilité par format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'round_brackets18549f92a457f2409'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMjwHLFQAAADMAAAATmNtYXDf7xCrAAABHAAAADxjdnQgBAkDLgAAAVgAAAASZ2x5ZmAOz2cAAAFsAAABJGhlYWQOKih8AAACkAAAADZoaGVhCvgVwgAAAsgAAAAkaG10eCA6AAIAAALsAAAADGxvY2EAAARLAAAC%2BAAAABBtYXhwBIgEWQAAAwgAAAAgbmFtZXHR30MAAAMoAAACOXBvc3QDogHPAAAFZAAAACBwcmVwupWEAAAABYQAAAAHAAAGcgGQAAUAAAgACAAAAAAACAAIAAAAAAAAAQIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAo8AMGe%2F57AAAHPgGyAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACACgAKf%2F%2FAAAAKAAp%2F%2F%2F%2F2f%2FZAAEAAAAAAAAAAAFUAFYBAAAsAKgDgAAyAAcAAAACAAAAKgDVA1UAAwAHAAA1MxEjEyMRM9XVq4CAKgMr%2FQAC1QABAAD%2B0AIgBtAACQBNGAGwChCwA9SwAxCwAtSwChCwBdSwBRCwANSwAxCwBzywAhCwCDwAsAoQsAPUsAMQsAfUsAoQsAXUsAoQsADUsAMQsAI8sAcQsAg8MTAREAEzABEQASMAAZCQ%2FnABkJD%2BcALQ%2FZD%2BcAGQAnACcAGQ%2FnAAAQAA%2FtACIAbQAAkATRgBsAoQsAPUsAMQsALUsAoQsAXUsAUQsADUsAMQsAc8sAIQsAg8ALAKELAD1LADELAH1LAKELAF1LAKELAA1LADELACPLAHELAIPDEwARABIwAREAEzAAIg%2FnCQAZD%2BcJABkALQ%2FZD%2BcAGQAnACcAGQ%2FnAAAQAAAAEAAPW2NYFfDzz1AAMIAP%2F%2F%2F%2F%2FVre7u%2F%2F%2F%2F%2F9Wt7u4AAP7QA7cG0AAAAAoAAgABAAAAAAABAAAHPv5OAAAXcAAA%2F%2F4DtwABAAAAAAAAAAAAAAAAAAAAAwDVAAACIAAAAiAAAAAAAAAAAAAkAAAAowAAASQAAQAAAAMACgACAAAAAAACAIAEAAAAAAAEAABNAAAAAAAAABUBAgAAAAAAAAABAD4AAAAAAAAAAAACAA4APgAAAAAAAAADAFwATAAAAAAAAAAEAD4AqAAAAAAAAAAFABYA5gAAAAAAAAAGAB8A%2FAAAAAAAAAAIABwBGwABAAAAAAABAD4AAAABAAAAAAACAA4APgABAAAAAAADAFwATAABAAAAAAAEAD4AqAABAAAAAAAFABYA5gABAAAAAAAGAB8A%2FAABAAAAAAAIABwBGwADAAEECQABAD4AAAADAAEECQACAA4APgADAAEECQADAFwATAADAAEECQAEAD4AqAADAAEECQAFABYA5gADAAEECQAGAB8A%2FAADAAEECQAIABwBGwBSAG8AdQBuAGQAIABiAHIAYQBjAGsAZQB0AHMAIAB3AGkAdABoACAAYQBzAGMAZQBuAHQAIAAxADgANQA0AFIAZQBnAHUAbABhAHIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlACAAUgBvAHUAbgBkACAAYgByAGEAYwBrAGUAdABzACAAdwBpAHQAaAAgAGEAcwBjAGUAbgB0ACAAMQA4ADUANABSAG8AdQBuAGQAIABiAHIAYQBjAGsAZQB0AHMAIAB3AGkAdABoACAAYQBzAGMAZQBuAHQAIAAxADgANQA0AFYAZQByAHMAaQBvAG4AIAAyAC4AMFJvdW5kX2JyYWNrZXRzX3dpdGhfYXNjZW50XzE4NTQATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlAAAAAAMAAAAAAAADnwHPAAAAAAAAAAAAAAAAAAAAAAAAAAC5B%2F8AAY2FAA%3D%3D)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%225.5%22%20y%3D%2216%22%3EP%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2215.5%22%20y%3D%2216%22%3E(%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2250.5%22%20y%3D%2216%22%3E)%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2222.5%22%20y%3D%2216%22%3EB%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22math1c8ffe9a587b126f152ed3d89a1%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2232.5%22%20y%3D%2216%22%3E%7C%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2241.5%22%20y%3D%2216%22%3EA%3C%2Ftext%3E%3Ctext%20fill%3D%22%2300007F%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2265.5%22%20y%3D%2216%22%3Eo%3C%2Ftext%3E%3Ctext%20fill%3D%22%2300007F%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2274.5%22%20y%3D%2216%22%3Eu%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2293.5%22%20y%3D%2216%22%3EP%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22104.5%22%20y%3D%2221%22%3EA%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22112.5%22%20y%3D%2216%22%3E(%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%22128.5%22%20y%3D%2216%22%3E)%3C%2Ftext%3E%3Ctext%20fill%3D%22%230000FF%22%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%22119.5%22%20y%3D%2216%22%3EB%3C%2Ftext%3E%3C%2Fsvg%3E) . .
|
|
 Vidéo de théorie et exercices-Espérance mathématique Vidéo de théorie et exercices-Espérance mathématique |
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous.
|
|
|
|
|
 Exercices de révision du chapitre 6 Exercices de révision du chapitre 6 |
Exercices de révision du chapitre 6 |
|
| Révision finale |
 Document de révision Document de révision |
Document de révision finale |
![\sqrt 3 = \sqrt[2] {3} = 3^{\frac {1}{2}}](http://recit.csbe.qc.ca/fel/math/math_img/913f00f943d3637447cca361372fc678.png)
![\sqrt {xy} = \sqrt[2] {xy} = (xy)^{\frac {1}{2}}](http://recit.csbe.qc.ca/fel/math/math_img/97d498592e7ca194dfa58036a7fe7d52.png)

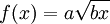 où a et b sont différents de zéro.
où a et b sont différents de zéro.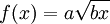
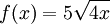
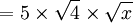
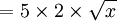
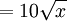
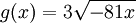
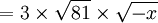
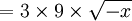
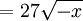
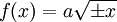 , il faut :
, il faut :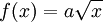 , si l'ouverture est vers la droite.
, si l'ouverture est vers la droite.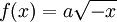 , si l'ouverture est vers la gauche.
, si l'ouverture est vers la gauche.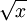 ou
ou ![\sqrt[2] {x}](http://recit.csbe.qc.ca/fel/math/math_img/c5b6de7f8df033feedb4ac12485487f2.png) pour exprimer la racine carrée de x.
pour exprimer la racine carrée de x.![\sqrt 4 = 4^{\frac {1}{2}}= \sqrt[2] {4}](http://recit.csbe.qc.ca/fel/math/math_img/3ef93790424ccf92118232b3fff32409.png)
![= \sqrt[2] {2^2} = 2](http://recit.csbe.qc.ca/fel/math/math_img/9c38f654408d076bb1338b3354aef82c.png) .
. ![\sqrt[n] {a^m} = a^{\frac {m}{n}}](http://recit.csbe.qc.ca/fel/math/math_img/85c88b44eee019603a6e7884c34a8050.png)
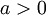
![\sqrt[8] {25^4} = 25^{\frac {4}{8}} = 25^{\frac {1}{2}} = 5](http://recit.csbe.qc.ca/fel/math/math_img/01eda4dc8defcbc1520b7feb66d76ac3.png)
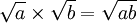
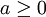
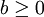
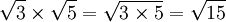
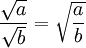
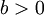
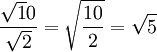

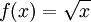 .
.