Vidéo de théorie et exercices-La droite de régression
|
1- Écouter la vidéo qui suit.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous. |
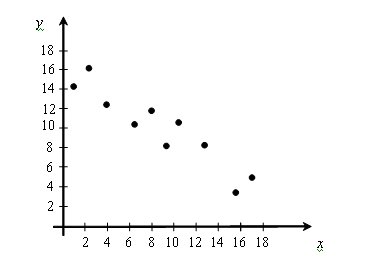
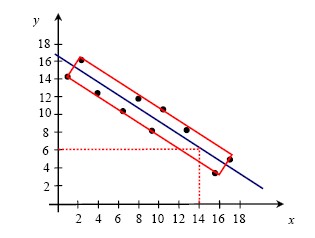
| À l'aide d'un tracé manuel de la droite, estime la valeur de la variable y lorsque la valeur de la variable x est 14. |  |
Lorsque la valeur de la variable x est 14, la valeur de la variable y est 6.
 |
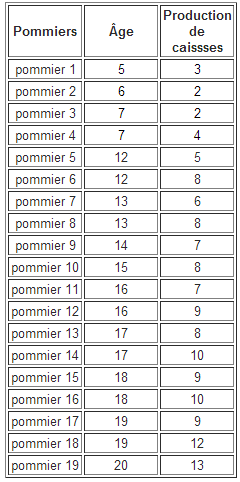
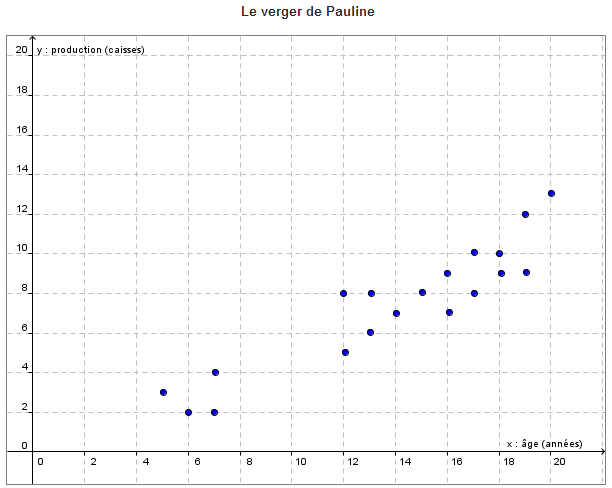
Le verger de Pauline compte 19 pommiers. Elle a noté dans un tableau et illustré à l'aide d'un nuage de points l'âge et la production de chacun. Estime l'âge d'un pommier qui produit 5 caisses de pommes.
|
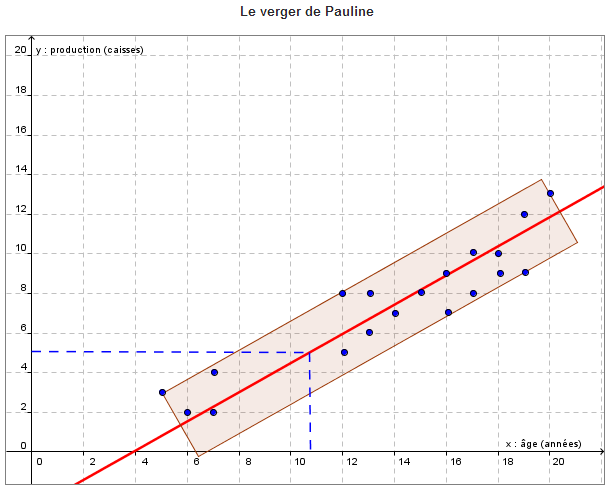
**Selon le graphique:**
Un pommier qui produit 5 caisses de pommes est âgé d’environ 10.5 ans.
**À l'aide de la droite de Mayer**
Posons:
x : âge en années
y : production de caisses
Nous trouvons la règle à partir des deux points moyenne. Il faut trouver la moyenne des points 1 à 10 et celle des points 10 à 19 car il y a un nombre impair de données.
(x1, y1)= (10,4 ; 5,3) et (x2, y2)= (17,5 ; 9,5)
La règle sera y = 0,59x - 0,84.
Lorsqu'on remplace y par 5 et qu'on isole x, on obtient x = 9,9.
**Un pommier qui produit 5 caisses de pommes est âgé d’environ 10 ans.**
**À l'aide de la calculatrice à affichage de graphiques:**
Nous trouvons la règle à partir de la calculatrice:
\(y =ax+b \)
avec \(a=0.6102\) et \(b=-1.1103\)
on remplace: a et b, ainsi que \(y=5\)
\(y =0.6102x-1.1103\)
\(5 =0.6102x-1.1103 \)
\(x=10.0136 \)
**Un pommier qui produit 5 caisses de pommes est âgé d’environ 10 ans.**
|
Voici les résultats de mathématiques d'un groupe de 10 élèves, à la fin de la 6e année du primaire, et à l'examen de fin d'année de mathématiques SN4. À la lumière de ces informations, quel serait le résultat à l'examen de mathématiques SN4 d'un élève ayant obtenu une note de 75% à la fin du primaire? Est-ce que cette estimation est relativement fiable? |
 |
| Note du primaire | Note de SN4 |
| 67 | 52 |
| 70 | 71 |
| 70 | 63 |
| 78 | 72 |
| 82 | 80 |
| 85 | 85 |
| 88 | 75 |
| 90 | 91 |
| 90 | 83 |
| 98 | 90 |
Avec la calculatrice
À l'aide de la calculatrice, je calcule premièrement le coefficient de corrélation.
J'obtiens r = 0,89, ce qui est une corrélation positive et forte me permettant de faire une estimation assez fiable.
L'équation de la droite de régression est y = 1,06x - 10,37.
Pour x = 75, la valeur de y est 69,13, donc l'élève aurait un résultat de 69%.
Avec la droite de Mayer
Les points moyenne sont (x1, y1)= (73,4 ; 67,6) et (x2, y2)= (90,2 ; 84,8)
L'équation de la droite est y = 1,02x - 7,6.
Pour x = 75, la valeur de y est 68,9, donc l'élève aurait un résultat de 69%.
***ATTENTION***
Toujours s'assurer que les données de la variable indépendante sont en ordre croissant avant de procéder aux calculs de la droite de Mayer.
Avec technologies.
Exemples 1 et 2
Exemple 3 et résumé.