Vidéo de théorie et exercices-Coefficient de corrélation
|
1- Écouter la vidéo qui suit.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous. |
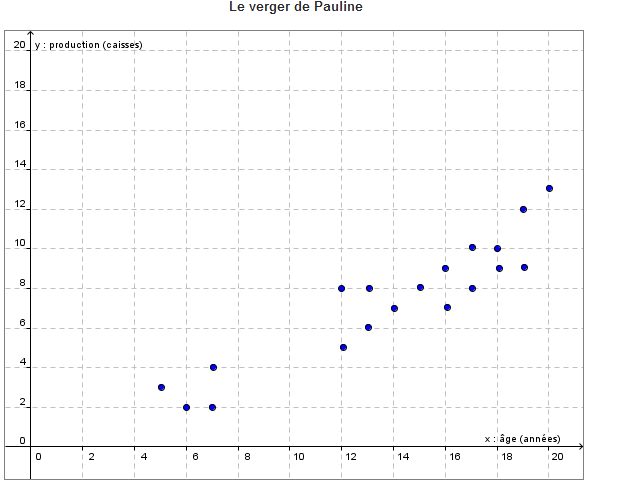
| Estime la valeur du coefficient de corrélation du nuage de points ci-dessous. Qualifie ensuite la corrélation. |  |
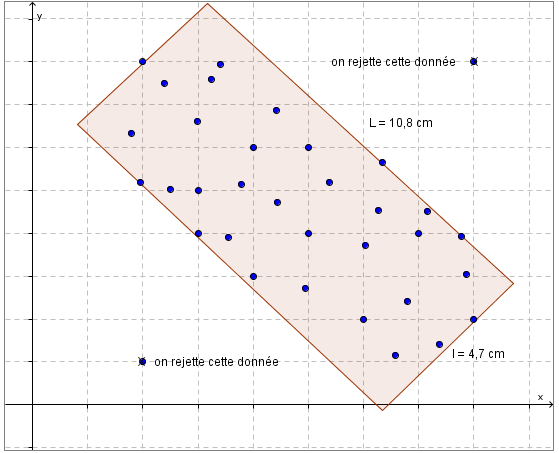
1) Tracer le plus petit rectangle qui englobe les points du nuage. Tu ne tiens pas compte des points qui s’éloignent significativement des autres points.
Voir graphique.
2) Mesurer la longueur du rectangle (L)
Voir graphique.
3) Mesurer la largeur du rectangle (l)
Voir graphique.
4) Utiliser la formule suivante pour effectuer le calcul du coefficient de corrélation (r).
\(r\approx\pm \left(1 - \frac{l}{L} \right)\)
\(r\approx\pm \left(1 - \frac{4,7}{10,8} \right)\)
\(r\approx\pm 0,56\)
5) Le coefficient de corrélation est positif (+) si le nuage est croissant et il est négatif (-) si le nuage de points est décroissant.
La valeur du coefficient de corrélation est négatif, car le nuage de points est décroissant.
Donc, r ≈ -0,56, ce qui est une corrélation négative et faible.
Plus la valeur de la variable x augmente, plus la valeur de la variable y diminue.
Si les points avaient été gradués, nous aurions pu trouver le coefficient à l'aide de la calculatrice à affichage de graphiques.

|
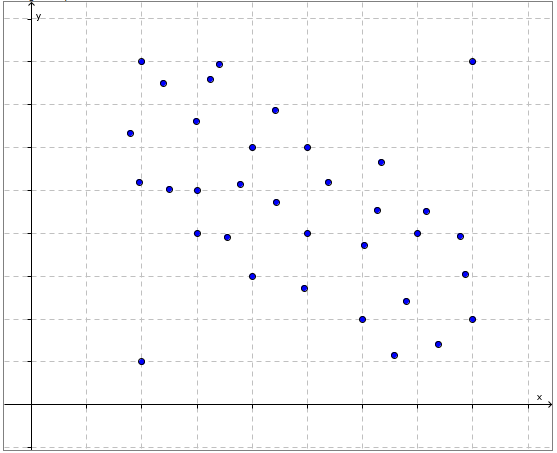
Le verger de Pauline compte 19 pommiers. Elle a noté dans un tableau et illustré à l’aide d’un nuage de points l’âge et la production de chacun.
|
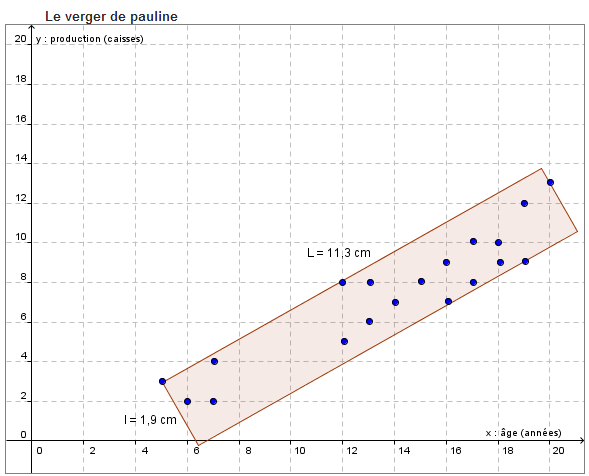
1) Tracer le plus petit rectangle qui englobe les points du nuage. Tu ne tiens pas compte des points qui s’éloignent significativement des autres points.
Voir graphique.
2) Mesurer la longueur du rectangle (L)
Voir graphique.
3) Mesurer la largeur du rectangle (l)
Voir graphique.
4) Utiliser la formule suivante pour effectuer le calcul du coefficient de corrélation (r).
\(r\approx \pm \left(1 - \frac{l}{L} \right)\)
\(r\approx\pm \left(1 - \frac{1,9}{11,3} \right)\)
\(r\approx\pm 0,83\)
5) Le coefficient de corrélation est positif (+) si le nuage est croissant et il est négatif (-) si le nuage de points est décroissant.
La valeur du coefficient de corrélation est positif, car le nuage de points est croissant.
Donc, r ≈ 0,83, ce qui est une corrélation positive et forte.
Plus le pommier est âgé, plus il produit de pommes.
Sachant que les points sont gradués, nous pouvons aussi trouver le coefficient de corrélation à l'aide de la calculatrice à affichage de graphiques.
Ainsi, \(r = 0,93\) avec la calculatrice.
|
Le tableau ci-dessous montre le salaire horaire moyen des hommes de 17 à 34 ans au Canada en 2011, selon le nombre d'années de scolarité complétées. Décris et interprète la corrélation entre le nombre d'années de scolarité et le salaire horaire moyen? |
 |
Pour qualifier la corrélation, il faut faire le nuage de points et calculer le coefficient de corrélation, sur papier ou avec un outil technologique.
Le coefficient de corrélation calculé à l'aide de la calculatrice est r = 0,92.
Cette corrélation est positive et forte.
Plus le nombre d'années de scolarité est élevé, plus le salaire horaire moyen est élevé.
 |
On a représenté le nombre d’années d’expérience et le salaire des employés de deux entreprises. Les données recueillies sont présentées dans ce nuage de points où x correspond au nombre d’années d’expérience et y correspond au salaire. |
Décris et interprète la corrélation entre ces variables.
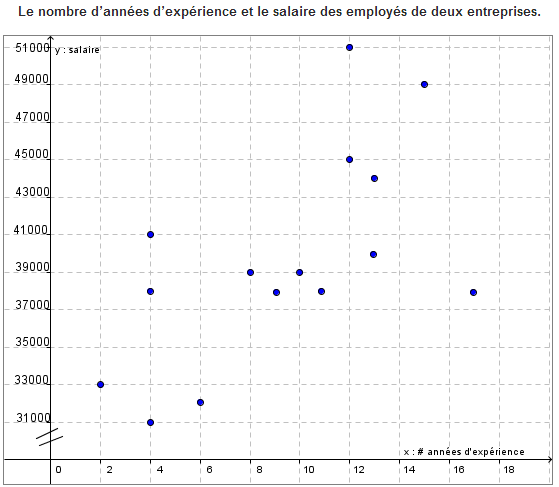
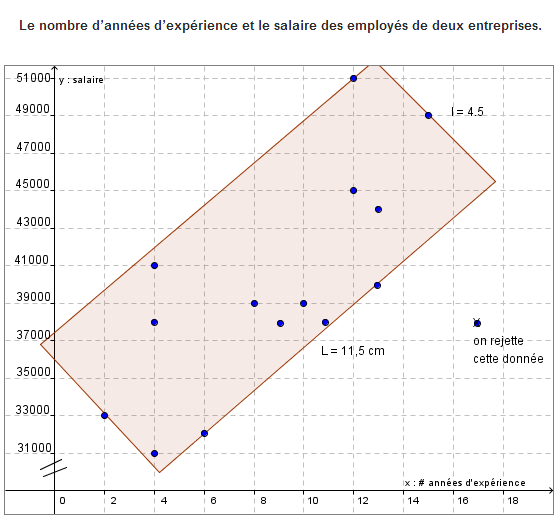
\(r\approx\pm \left(1 - \frac{l}{L} \right)\)
\(r\approx\pm \left(1 - \frac{4,5}{11,5} \right)\)
\(r\approx\pm 0,61\)
r ≈ 0,61
**Selon la calculatrice:**
\(r = 0,74\)
**La corrélation est positive et moyenne. Plus le nombre d'années d'expérience augmente, plus le salaire augmente**.
Ordonne les coefficients de corrélation linéaires suivants du plus fort au plus faible.
-0,27 0,55 -0,91 -0,12 0,7
-0,91 0,7 0,55 -0,27 -0,12
Méthode du rectangle à la main
Méthodes avec calculatrice graphique et logiciel Geogebra
Exemples 1, 2 et 3