Vidéo de théorie et exercices-Loi des sinus
 |
Résous le triangle ABC suivant. Donne tes réponses arrondies au dixième près pour les côtés et pour les angles. |
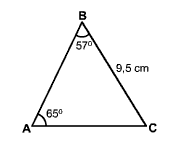
\(m\;\angle\;C = 180^\circ - m\;\angle\;A - m\;\angle\;B\)
\(m\;\angle\;C = 180^\circ - 65^\circ - 57^\circ\)
\(m\;\angle\;C = 58^\circ\) car la somme des angles d’un triangle est de 180°.
\(m\;\overline {AC} = b\) et, par la loi des sinus :
\(\frac {a}{\sin A} = \frac {b}{\sin B}\)
//a// (9,5 cm) représente le côté opposé à l’angle A (65°) et
//b// représente le côté opposé à l’angle B (57°).
\(\frac {9,5}{\sin 65^\circ} = \frac {b}{\sin 57^\circ}\) en remplaçant les valeurs connues.
\(9,5 \times \sin 57^\circ = b \times \sin 65^\circ\) car le produit des extrêmes égale le produit des moyens.
\(\frac {9,5 \times \sin 57^\circ}{\sin 65^\circ} = b\) en divisant chaque membre de l’équation par \(\sin 65^\circ\) pour isoler //b//.
\(b \approx 8,8 cm\)
\(m\;\overline {AB} = c\) et, par la loi des sinus :
\(\frac {a}{\sin A} = \frac {c}{\sin C}\)
//a// (9,5 cm) représente le côté opposé à l’angle A (65°) et
//c// représente le côté opposé à l’angle C (58°).
\(\frac {9,5}{\sin 65^\circ} = \frac {c}{\sin 58^\circ}\) en remplaçant les valeurs connues.
\(9,5 \times \sin 58^\circ = c \times \sin 65^\circ\) car le produit des extrêmes égale le produit des moyens.
\(\frac {9,5 \times \sin 58^\circ}{\sin 65^\circ} = c\) en divisant chaque membre de l’équation par \(\sin 65^\circ\) pour isoler //c//.
\(c \approx 8,9 cn\)
 |
Résous le triangle ABC suivant. Donne tes réponses arrondies au dixième près pour les côtés et pour les angles.
|
Par la loi des sinus :
\(\frac {a}{\sin A} = \frac {b}{\sin B}\)
a (5,5) représente le côté opposé à l’angle A (19°) et
b (14,7) représente le côté opposé à l’angle B.
\(\frac {5,5}{\sin 19^\circ} = \frac {14,7}{\sin B}\) en remplaçant les valeurs connues.
\(5,5 \times \sin B = 14,7 \times \sin 19^\circ\) car le produit des extrêmes égale le produit des moyens.
\(\sin B = \frac {14,7 \times \sin 19^\circ}{5,5}\) en divisant chaque membre de l’équation par 5,5 pour isoler sin B.
\(\sin B = 0,87\)
\(m\;\angle\;B = \sin ^{-1}(0,87)\) en isolant l’angle B.
\(m\;\angle\;B \approx 60,5^\circ\)
ATTENTION! L’angle B ne peut pas mesurer 60,5°, car c’est un angle obtus.
Ainsi, il faut faire cette soustraction :
\(m\;\angle\;B = 180^\circ - 60,5^\circ\)
\(m\;\angle\;B = 119,5^\circ\)
\(m\;\angle\;C = 180^\circ - m\;\angle\;A - m\;\angle\;B\)
\(m\;\angle\;C = 180^\circ - 119,5^\circ - 19^\circ\)
\(m\;\angle\;C = 41,5^\circ\)
car la somme des angles d’un triangle est de 180°.
Par la loi des sinus :
\(\frac {a}{\sin A} = \frac {c}{\sin C}\)
a (5,5) représente le côté opposé à l’angle A (19°) et
c représente le côté opposé à l’angle C (41,5°).
\(\frac {5,5}{\sin 19^\circ} = \frac {c}{\sin 41,5^\circ}\) en remplaçant les valeurs connues.
\(5,5 \times \sin 41,48^\circ = c \times \sin 19^\circ\) car le produit des extrêmes égale le produit des moyens.
\(\frac {5,5 \times \sin 41,48^\circ}{\sin 19^\circ} = c\) en divisant chaque membre de l’équation par \(\sin 19^\circ\) pour isoler c.
\(c \approx 11,2\) cm.
|
Voici le plan d'une terrasse. Cette dernière forme un parallélogramme ABCD. La grande diagonale AC mesure 16 mètres et les angles qu'elle forme avec les côtés sont respectivement de 30° et de 35°. On désire clôturer cette terrasse. Trouve la longueur totale de cette clôture. Arrondis ta réponse au dixième près. |
 |
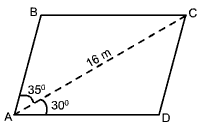
Pour trouver le périmètre de la terrasse, il faut trouver \(m\;\overline {AD}\) et \(m\;\overline {CD}\) dans le triangle ACD. Par la suite, on multipliera par deux la somme de ces côtés.
\(m\;\angle\;ACD = 35^\circ\) car les angles BAC et ACD sont des angles alternes-internes congrus.
\(m\;\angle\;ADC = 115^\circ\) :
\(m\;\angle\;ADC = 180^\circ - m\;\angle\;CAD - m\;\angle\;ACD\)
\(m\;\angle\;ADC = 180^\circ - 30^\circ - 35^\circ\)
\(m\;\angle\;ADC = 115^\circ\)
car la somme des angles d’un triangle est de 180°.
\(m\;\overline {CD} = a\)
Par la loi des sinus :
\(\frac {a}{\sin A} = \frac {d}{\sin D}\)
a représente le côté opposé à l’angle A (30°) et
d (16 m) représente le côté opposé à l’angle D (115°).
\(\frac {a}{\sin 30^\circ} = \frac {16}{\sin 115^\circ}\) en remplaçant les valeurs connues.
\(a \times \sin 115^\circ = 16 \times \sin 30^\circ\) car le produit des extrêmes égale le produit des moyens.
\(a = \frac {16 \times \sin 30^\circ}{\sin 115^\circ}\) en divisant chaque membre de l’équation par \(\sin 115^\circ\) pour isoler a.
\(a \approx 8,8m\)
\(m\;\overline {AD} = c\)
Par la loi des sinus :
\(\frac {c}{\sin C} = \frac {d}{\sin D}\)
c représente le côté opposé à l’angle C (35°) et
d (16 m) représente le côté opposé à l’angle D (115°).
\(\frac {c}{\sin 35^\circ} = \frac {16}{\sin 115^\circ}\) en remplaçant les valeurs connues.
\(c \times \sin 115^\circ = 16 \times \sin 35^\circ\) car le produit des extrêmes égale le produit des moyens.
\(c = \frac {16 \times \sin 35^\circ}{\sin 115^\circ}\) en divisant chaque membre de l’équation par \(\sin 115^\circ\) pour isoler c.
\(c \approx 10,1m\)
Ainsi, le périmètre sera :
\((m\;\overline {CD} \approx 8,8 + m\;\overline {AD} \approx 10,1) \times 2 = 37,8 m\)
La longueur totale de la clôture sera d’environ 37,8 mètres.
|
Denis et Magalie regardent le haut d'un édifice. Denis observe le sommet de l'édifice sous un angle d'élévation de 40 degrés. Magalie est à 58 mètres de Denis et elle observe le sommet de l'édifice sous un angle d'élévation de 70 degrés. Quelle est la hauteur de l'édifice? Arrondis ta réponse au mètre près. |
 |
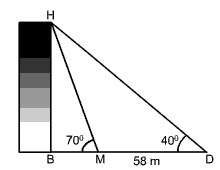
Pour trouver la hauteur de l’édifice \(m\;\overline {BH}\) il faut trouver l’hypoténuse \(m\;\overline {HM}\) du triangle BHM.
Pour trouver la mesure du segment \(m\;\overline {HM}\) on utilisera la loi des sinus dans le triangle DHM.
Ensuite, on utilisera les rapports trigonométriques dans le triangle rectangle BHM pour trouver la hauteur de l’édifice \(m\;\overline {BH}\)
\(m\;\angle\;DMH = 180^\circ - 70^\circ\)
\(m\;\angle\;DMH = 110^\circ\)
car les angles BMH et DMH sont supplémentaires.
\(m\;\angle\;DHM = 180^\circ - 110^\circ - 40^\circ\)
\(m\;\angle\;DHM = 30^\circ\)
car la somme des angles du triangle DHM est de 180°.---
La mesure du côté HM = 74,6 m, par la loi des sinus :
\(\frac {h}{\sin H} = \frac {d}{\sin D}\)
h (58 m) représente le côté opposé à l’angle H (30°) et
d représente le côté opposé à l’angle D (40°).
\(\frac {58}{\sin 30^\circ} = \frac {d}{\sin 40^\circ}\) en remplaçant les valeurs connues.
\(58 \times \sin 40^\circ = d \times \sin 30^\circ\) car le produit des extrêmes égale le produit des moyens.
\(\frac {58 \times \sin 40^\circ}{\sin 30^\circ} = d\) en divisant chaque membre de l’équation par \(\sin 30^\circ\) pour isoler d.
\(74,6 \approx d\)
La mesure du côté BH = 70,1 m, par le rapport trigonométrique //**sin**// (triangle rectangle) :
![]()
\(\sin 70^\circ = \frac {x}{74,6}\) en remplaçant les valeurs connues.
\(74,6 \times \sin 70^\circ = x\) en multipliant chaque membre de l’équation par 74,6.
\(70,1 \approx x\) par multiplication.
Donc, la hauteur de l’édifice est d’environ 70 mètres.
 |
Résous le triangle FRE suivant. Donne tes réponses arrondies au dixième près pour les côtés et pour les angles. |
1) Trouver la mesure de l'angle R
Avec la loi des sinus,
\(\frac {f}{\sin F} = \frac {r}{\sin R}\)
\(\frac {9}{\sin 30^\circ} = \frac {14}{\sin R}\) en remplaçant les valeurs connues.
\(9 \times\sin R= 14 \times \sin 30^\circ\) car le produit des extrêmes égale le produit des moyens.
\(\sin R = 0,78\)
\(m\;\angle\;R = \sin ^{-1}(0,78)\) en isolant l’angle R.
\(m\;\angle\;R \approx 51,3^\circ\)
2) Trouver la mesure de l'angle E
\(m\;\angle\;E \approx 98,7^\circ\) car la somme des angles intérieurs d'une triangle est 180o.
3) Trouver la mesure du côté FR
\(\frac {e}{\sin E} = \frac {f}{\sin F}\)
\(\frac {e}{\sin 98,7} = \frac {9}{\sin 30}\)
\(9 \times\sin 98,7=e \times \sin 30^\circ\) car le produit des extrêmes égale le produit des moyens.
\(m\;\overline {FR} \approx 17,8 cm\)