Vidéo de théorie et exercices-Relations métriques dans le triangle rectangle
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous. |
|
Dans ce triangle rectangle ABC, le segment AB mesure 7 cm et le segment AC mesure 10,63 cm. Détermine la mesure du segment CD en justifiant tes calculs. |
 |
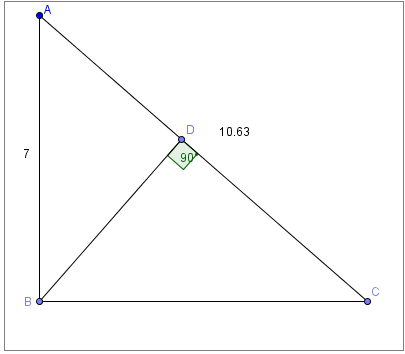
1) Trouver la mesure du côté BC à l'aide de la relation de Pythagore
c² = a² + b²
10,63² = 7² + b²
La mesure de "b" est de 8 unités, donc la mesure du côté BC est 8 unités.
2) Trouver la mesure du segment CD à l'aide du théorème des projections sur l'hypoténuse.
\(\frac{c_1}{a}=\frac{a}{c}\) ou a² = c1 x c
nous obtenons la relation suivante :
\(\frac{m \overline{CD}}{8}=\frac{8}{10,63}\) ou \(8^2=10,63*m\overline{CD} \)
\(64=10,63*m\overline{CD}\)
\(m\overline{CD}=6,02\) unités.
 |
Dans le triangle de la question 1, calcule la mesure de la hauteur relative à l'hypothénuse en justifiant tes calculs. |
**À l'aide du théorème du produit des cathètes:**
\(\frac{C_1}{Hyp}=\frac{H}{C_2}\),
nous obtenons la relation suivante :
\(m\overline{AB}*m\overline{BC}=m\overline{AC}*m\overline{BD}\)
\(7*8=10,63*m\overline{BD}\)
\(m\overline{BD}=5,27cm\)
| Calcule la valeur du segment BC en justifiant tes calculs. |  |
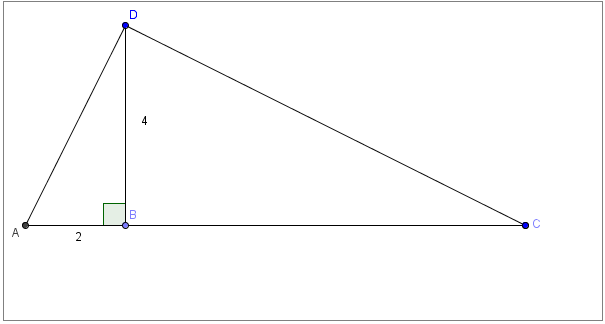
**À l'aide du théorème de la hauteur relative à l'hypoténuse :**
\(\frac{c_1}{h}=\frac{h}{c_2}\) OU h² = c1 x c2
nous obtenons la relation suivante:
\(\frac 24=\frac{4}{m\overline{BC}}\)
\(4^2=2*m\overline{BC}\)
\(16=2*m\overline{BC}\)
\(8=m\overline{BC}\)
 |
Trouve la valeur de chaque mesure manquante et donne l'énoncé qui supporte ce calcul. Trouve la mesure de b,c et e. |
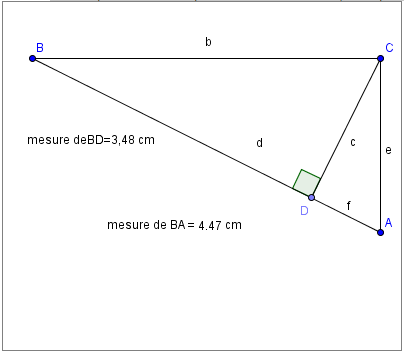
1) Mesure du côté BC = 3,94 cm, selon le **théorème des projections sur l'hypoténuse.**
\(\frac{c_1}{a}=\frac{a}{c}\) OU a² = c1 x c
\(\frac{3,48}{a}=\frac{a}{4,47}\)
\(a^2=3,48 \cdot 4,47\)
\(a=3,94cm\)
2)Mesure de la hauteur CD = 1,86 cm, selon le **théorème de la hauteur relative à l'hypoténuse.**
\(\frac{c_1}{h}=\frac{h}{c_2}\) OU h² = c1 x c2
\(\frac{3,48}{h}=\frac{h}{4,47-3,48}\)
\(h^2=3,48\cdot 0,99\)
\(h=1,86\)
3) Mesure du côté AC = 2,11 cm, selon le théorème de Pythagore.
Attention : Sachant que vous êtes dans un triangle rectangle vous pouvez toujours utiliser le théorème de Pythagore lorsqu'il est applicable!
 |
L'aire du triangle EKO est de 71,81 mm². La mesure du côté EK est de 14,36 mm. Trouve la mesure de tous les autres segments du triangle. Justifie chacun de tes calculs. |
1) L'aire étant de 71,81 mm², on peut trouver la mesure du côté KO.
Aire d'un triangle = (base x hauteur)/2
71,81 = (\(m \overline{KO}\) x 14,36)/2
\(m \overline{KO}\) = 10 mm
2) À l'aide de la relation de Pythagore, on peut trouver la mesure du côté EO.
c ² = a² + b²
c² = 14,36² + 10²
c = 17,5 mm
\(m \overline{EO}\) = 17,5 mm
3) À l'aide du théorème du produit des cathètes, on peut trouver la mesure de la hauteur KT.
a x b = h x c
14,36 x 10 = h x 17,5
8,2 = h
\(m \overline{KT}\) = 8,2 mm
4) À l'aide de la relation de Pythagore, on peut trouver les mesure des segments ET et TO.
\(m \overline{ET}\) = 11,8 mm
\(m \overline{TO}\) = 5,7mm
 |
Quel est le périmètre du ΔCRT? |
1) La mesure du côté RT est 6,3 cm par Pythagore dans ΔRLT.
2) La mesure du segment CL est 10,1 cm par le théorème de la hauteur dans ΔCRT.
3) La mesure du côté CR est 11,5 cm par Pythagore dans ΔCLR.
4) La mesure du côté CT est 13,1 cm par addition.
5) Le périmètre du ΔCRT est 30,9 cm.
|
Dans le ΔNOR, la mesure du côté NR est 15 mètres et celle de la hauteur OD, 6,77m. Quelle est, au dixième près, la mesure du côté NO? |
 |
1) Dans ce problème, nous sommes dans l'impossibilité d'utiliser un des théorèmes connus. Il faut utiliser une nouvelle astuce pour pouvoir se servir du théorème de la hauteur par la suite. Il s'agit de poser que la mesure du segment ND vaut x, et celle de DR, 15 - x.
Théorème de la hauteur: h² = c1 x c2
6,77² = x (15 - x)
45,8 = 15x - x²
x² - 15x + 45,8 = 0 C'est une équation du 2e degré à résoudre.
2) Utiliser la formule quadratique pour trouver les valeurs de x possibles.
\(x=\frac {-b \pm \sqrt {b^2 - 4ac}}{2a}\)
\(x=\frac {-(-15) \pm \sqrt {(-15)^2 - 4(1)(45,8)}}{2}\)
\(x=\frac {15 \pm \sqrt {41,8}}{2}\)
x1 = 10,73m (mesure du segment DR) et x2 = 4,27m (mesure du segment ND)
3) Mesure du côté NO = 8 m. (En utilisant Pythagore dans le ΔNDO)
Théorème de la hauteur.
Théorème des projections sur l'hypoténuse.
Théorème du produit des cathètes.
Résumé et exemples.