Vidéo de théorie et exercices-Triangles rectangles (rapports trigonométriques)
|
1- Écouter la vidéo ci-dessous.
Si tu le préfères, tu peux écouter la vidéo par parties.
Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices.
2- Répondre aux exercices sur du papier.
Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous.
3- Corriger les exercices.
Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous. |
| Résous le triangle rectangle ABC suivant. Donne tes réponses arrondies au dixième près pour les côtés et pour les angles. | 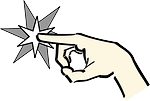 |
\(m\;\overline {AC} = 3,6\;cm\), par le rapport trigonométique **tan** :
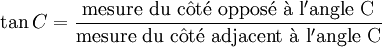
\(\tan 59^\circ = \frac {6}{m\;\overline {AC}}\), en remplaçant les valeurs connues.
\(m\;\overline {AC} \times \tan 59^\circ = 6\), en multipliant chaque membre de l’équation par \(m\;\overline {AC}\)
\(m\;\overline {AC} = \frac {6}{\tan 59^\circ}\), en divisant chaque membre de l’équation par \(\tan 59^\circ\).
\(m\;\overline {AC} = 3,6\;cm\), en arrondissant au dixième près.
\(m\;\overline {BC} = 7\;cm\), par la relation de Pythagore
\(m\;\overline {BC}^2 = m\;\overline {AC}^2 + m\;\overline {AB}^2\)
\(m\;\overline {BC}^2 = 3,6^2 + 6^2\), en remplaçant les valeurs connues.
\(m\;\overline {BC}^2 = 48,96\), par addition.
\(m\;\overline {BC} = \sqrt {48,96}\), en isolant \(m\;\overline {BC}\)
\(m\;\overline {BC} = 7\), en arrondissant au dixième près.
\(m\;\angle\;B = 31^\circ\) :
\(m\;\angle\;B = 90^\circ - m\;\angle\;C\)
\(m\;\angle\;B = 90^\circ - 59^\circ = 31^\circ\), car les angles aigus d’un triangle rectangle sont complémentaires.
 |
Résous le triangle rectangle ABC suivant. Donne tes réponses arrondies au dixième près pour les côtés et pour les angles.
|
\(m\;\angle\;A = 40,1^\circ\), par le rapport trigonométrique **cos** :
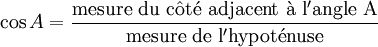
\(\cos A = \frac {6,5}{8,5}\), en remplaçant les valeurs connues.
\(A = cos^{-1} \left( \frac {6,5}{8,5} \right)\), en isolant l'angle A.
\(A = 40,1^\circ \), en arrondissant au dixième près.
\(m\;\angle\;B = 49,9^\circ\) :
\(m\;\angle\;B = 90^\circ - m\;\angle\;A\)
\(m\;\angle\;B = 90^\circ - 40,1^\circ = 49,9^\circ\), car les angles aigus d’un triangle rectangle sont complémentaires.
\(m\;\overline {BC} = 5,5\;cm\), par la relation de Pythagore :
\(m\;\overline {AB}^2 = m\;\overline {AC}^2 + m\;\overline {BC}^2\)
\(8,5^2 = 6,5^2 + m\;\overline {BC}^2\), en remplaçant les valeurs connues.
\(8,5^2 - 6,5^2 = m\;\overline {BC}^2\), en soustrayant 6,5² aux deux membres de l’équation.
\(\sqrt {8,5^2 - 6,5^2} = m\;\overline {BC}\), en isolant \(m\;\overline {BC}\)
\(5,5 = m\;\overline {BC}\), en arrondissant au dixième près (n'oubliez pas les parenthèses!).
| Une échelle de 10 m est appuyée contre un mur de façon à former un angle de 70° avec le sol. À quelle distance du mur se trouve l’échelle? Arrondis ta réponse au dixième près. | 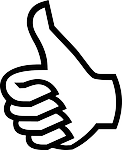 |
Pour trouver la distance entre l’échelle et le mur, il faut utiliser le rapport trigonométrique cos, car on connaît la mesure du côté adjacent à l’angle de 70° et l’hypoténuse :
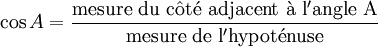
\(\cos 70^\circ = \frac {x}{10}\), en remplaçant les valeurs connues.
\(10 \times \cos 70^\circ = x\), en multipliant chaque membre de l’équation par 10.
\(3,42 \approx x\), par multiplication.
**Donc, la distance entre l’échelle et le mur est d’environ 3,4 m.**
|
Dans la figure présentée au numéro 3, un homme monte jusqu’au bout de l’échelle. À quelle hauteur du sol se trouve-t-il? Arrondis ta réponse au dixième près. |
 |
Pour trouver la distance entre l’homme et le sol, on peut utiliser les rapports trigonométriques sin ou tan, ou la relation de Pythagore :
\(\sin 70^\circ = \frac {x}{10}\), en remplaçant les valeurs connues.
\(10 \times \sin 70^\circ = x\), en multipliant chaque membre de l’équation par 10.
\(9,39 \approx x\), par multiplication.
**Donc, la distance entre l’homme et le sol est d’environ 9,4 m**.
 |
À un moment de la journée, l’ombre projetée sur le sol par un édifice d’une hauteur de 200 m mesure 40 m. Quelle est la mesure de l’angle d’élévation du soleil? Arrondis ta réponse au degré près. N.B. L'angle d'élévation est l'angle formé par l'horizontale et la ligne de visée, lorsqu'un objet observé est plus haut que la personne qui observe. |
Pour trouver l’angle d’élévation du soleil, il faut utiliser le rapport trigonométrique tan, car on connaît la mesure du côté opposé et la mesure un côté adjacent à l’angle recherché.
![]()
\(\tan A = \frac {200}{40}\), en remplaçant les valeurs connues.
\(A = tan^{-1} \left( \frac {200}{40} \right)\), en isolant l'angle A.
\(A \approx 78,69^\circ \), n’oubliez pas de mettre les parenthèses.
**Donc, la mesure de l’angle d’élévation du soleil est d’environ 79°.**
 |
Dans le triangle FJU, la mesure du segment FH est de 15 cm et la mesure de l'angle F est de 32o. Les angles J et H sont droits. Quelle est la mesure du segment HU? |
1) Dans le ΔFHJ, la mesure de l'angle FJH est de 58o.
(Angles aigus complémentaires dans un triangle rectangle)
2) Dans le ΔFHJ,
\(\tan 32^\circ = \frac {m\;\overline {JH}}{m\;\overline {FH}}\)
\(\tan 32^\circ = \frac {m\;\overline {JH}}{15}\)
\(m\;\overline {JH}\)= 9,37 cm
3) Dans le ΔJHU, la mesure de l'angle HJU est de 32o.
(Angle complémentaire à l'angle FJH de 58o)
4) Dans le ΔJHU,
\(\tan 32^\circ = \frac {m\;\overline {HU}}{m\;\overline {JH}}\)
\(\tan 32^\circ = \frac {m\;\overline {HU}}{9,37}\)
\(m\;\overline {HU}\)= 5,86 cm
|
Laura prend une marche avec son chien. Au même moment, ils aperçoivent un os par terre. Laura, d'une taille de 1,65 m, voit l'os sous un angle de dépression de 29o. Elle est à ce moment à une distance de 2,4 m de son chien. Au moment où les deux aperçoivent l'os, quelle est la distance entre le chien et l'os et aussi, quelle est la grandeur(hauteur) du chien? |
N.B. L'angle de dépression est l'angle formé par l'horizontale et la ligne de visée, lorsqu'un objet observé est plus bas que la personne qui observe.
1) Dans le grand triangle, on peut trouver la distance entre Laura et l'os car on a un angle et un côté.
On nommera cette distance "d".
\(tan 29= \frac{1,65}{d}\)
La mesure de "d" est 2,98 m.
On peut maintenant déduire la distance entre le chien et l'os: x = 2,98 - 2,4
x = 0,58 m
2) Dans le petit triangle, on peut trouver la mesure de la 2e cathète car on a un angle et une cathète.
On nommera cette cathète "c".
\(tan 29= \frac{c}{2,4}\)
La mesure de "c" est 1,33 m.
On peut maintenant déduire la grandeur du chien: y = 1,65 - 1,33
y = 0,32 m
Rappel, théorie et exemple 1.
Exemples 2,3 et 4: recherche d'un côté manquant.
Exemples 4 à 8: recherche d'un angle manquant et résolution d'un triangle.