Vidéo de théorie et exercices-Fonction polynominale de degré 2 (quadratique)
|
1- Écouter la vidéo ci-dessous. Si tu le préfères, tu peux écouter la vidéo par parties. Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices. 2- Répondre aux exercices sur du papier. Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous. 3- Corriger les exercices. Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous. |
 |
Quelles sont les coordonnées du sommet des paraboles d’équations suivantes? a) \(f(x) = 4(x - 2)^2 + 7\) b) \(g(x) = -(x + 3)^2 + 2\) c) \(h(x) = 3(x + 5)^2 - 3\) d) \(p(x) = x^2 + 6x - 3\) e) \(q(x) = 3x^2 - 12x\) f) \(r(x) = -x^2 + 4x\) |
a)
\(f(x) = 4(x - 2)^2 + 7\)
**Sommet : (2, 7)**
b)
\(g(x) = -(x + 3)^2 + 2\)
**Sommet : (-3, 2) car \(g(x) = -(x - -3)^2 + 2\)**
c)
\(h(x) = 3(x + 5)^2 - 3\)
**Sommet : (-5, -3) car \(h(x) = 3(x - -5)^2 - 3\)**
d)
\(p(x) = x^2 + 6x - 3\)
**Sommet : (-3, -12) car sa forme canonique est \(p(x) = 1(x + 3)^2 - 12\)**
e)
\(q(x) = 3x^2 - 12x\)
**Sommet : (2, -12) car sa forme canonique est \(q(x) = 3(x - 2)^2 - 12\)**
f)
\(r(x) = -x^2 + 4x\)
**Sommet : (2 ,4) car sa forme canonique est \(r(x) = -1(x - 2)^2 + 4\)**
 |
Les paraboles d’équations suivantes sont-elles ouvertes vers le haut ou vers le bas? Quelle est l’équation de leur axe de symétrie?
\(f(x) = 2(x - 6)^2 + 5\)
\(g(x) = -(x + 7)^2 - 3\)
\(h(x) = -4x^2 + 12x - 8\)
\(p(x) = x^2 - 3x + 5\) |
a)
\(f(x) = 2(x - 6)^2 + 5\)
**Ouverte vers le haut, car a est positif. Équation de l'axe de symétrie : x = 6 car h = 6**
b)
\(g(x) = -(x + 7)^2 - 3\)
**Ouverte vers le bas, car a est négatif. Équation de l'axe de symétrie : x = -7 car h = -7**
c)
\(h(x) = -4x^2 + 12x - 8\)
**Ouverte vers le bas, car a est négatif. Équation de l'axe de symétrie : x = \(\frac {3}{2}\) car h = \(\frac {3}{2}\)**
d)
\(p(x) = x^2 - 3x + 5\)
**Ouverte vers le haut, car a est positif. Équation de l'axe de symétrie : x = \(\frac {3}{2}\) car h = \(\frac {3}{2}\)**
 |
Écris les fonctions quadratiques suivantes sous la forme générale. a) \(f(x) = (x - 5)^2 + 3\) b) \(g(x) = -3(x + 2)^2 - 5\) c) \(h(x) = \frac {2}{3}(x - 3)^2 + 2\) |
a)
\(f(x) = x^2 -10x + 28\)
b)
\(g(x) = -3x^2 -12x -17\)
c)
\(h(x) = \frac {2}{3}x^2 - 4x + 8\)
Écris les équations suivantes sous la forme canonique.
a)
\(f(x) = 5x^2 - 60x + 184\)
b)
\(g(x) = -3x^2 - 6x + 7\)
c)
\(h(x) = -\frac {1}{3}x^2 + 2x - 4\)
a)
\(f(x) = 5(x - 6)^2 + 4\)
b)
\(g(x) = -3(x + 1)^2 + 10\)
c)
\(h(x) = -\frac {1}{3}(x - 3)^2 - 1\)
 |
Écris l'équation suivante sous la forme générale et canonique. \(f(x) = -2(x + 3)(x - 5)\) Ensuite, effectue l'étude complète: domaine, image, coordonnées à l'origine, extremum, variation, signe et axe de symétrie. |
La forme générale est :
\(f(x) = -2x^2 + 4x + 30\)
La forme canonique est :
\(f(x) = -2(x - 1)^2 + 32\)
Étude:
Domaine: xε ]-∞,+∞[
Image: yε ]-∞,32]
Ordonnée à l'origine: f(0)=30
Abscisses à l'origine: x1=-3 et x2= 5
Axe de symétrie: x = 1
Maximum: y=32
Minimum: Aucun
Variation: f(x) est croissante pour xε ]-∞,1] et décroissante pour xε [1,+∞[
Signe: f(x)>0 pour xε [-3, 5] et f(x)<0 pour xε ]-∞,-3] U [5, +∞[
Trace les fonctions quadratiques suivantes.
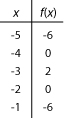
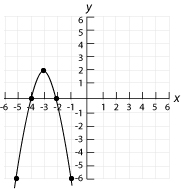
a) \(f(x) = -2x^2 - 12x - 16\)
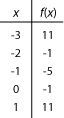
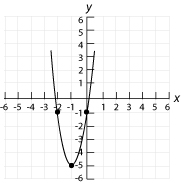
b) \(g(x) = 4x^2 + 8x - 1\)
a) Son sommet est : (-3, 2)
 |
 |
b) Son sommet est : (-1, -5)
 |
 |
Indique quelle forme, canonique, générale ou factorisée, est utilisée pour déterminer le plus facilement :
a) le sommet d’une parabole
b) l’axe de symétrie d’une parabole
c) l’ouverture d’une parabole
d) les zéros d'une parabole
e) l’ordonnée à l’origine d’une parabole
a) le sommet d’une parabole, **c'est la forme canonique**
b) l’axe de symétrie d’une parabole, **c'est la forme canonique**
c) l’ouverture d’une parabole, **c'est l'une ou l'autre, car le coefficient a de la générale et de la factorisée est de même valeur que le paramètre a de la canonique**
d) les zéros d'une parabole, **c'est la forme factorisée**
e) l’ordonnée à l’origine d’une parabole, **c'est la forme générale avec le terme constant c**
À partir du graphique de la fonction quadratique de base f(x) = x², décris les transformations pour obtenir chacune des règles ci-dessous.
a)
\(g(x) = (x - 5)^2\)
b)
\(h(x) = \frac {1}{4}(x + 1)^2\)
c)
\(j(x) = (x + 2)^2 + 3\)
d)
\(k(x) = 4x^2 - 5\)
e)
\(l(x) = -3(x - 4)^2 + 5\)
a)
\(g(x) = (x - 5)^2\)
**une translation de 5 unités vers la droite**
b)
\(h(x) = \frac {1}{4}(x + 1)^2\)
**changement d’échelle vertical de (1/4) et translation de 1 unité vers la gauche**
c)
\(j(x) = (x + 2)^2 + 3\)
**translation de 2 unités vers la gauche et de 3 unités vers le haut**
d)
\(k(x) = 4x^2 - 5\)
**changement d’échelle vertical de 4 et translation de 5 unités vers le bas**
e)
\(l(x) = -3(x - 4)^2 + 5\)
**changement d’échelle vertical de 3 et réflexion sur l'axe y=5 ainsi que translation de 4 unités vers la droite et de 5 unités vers le haut**
Voici les règles de différentes fonctions quadratiques.
\(y_1 = x^2 - 100x\)
\(y_2 = 0,25x^2 + x - 1\)
\(y_3 = 5x^2 + 3x + 32\)
\(y_4 = -100x^2\)
a) Laquelle de ces fonctions s'associe à la parabole la plus ouverte?
b) Quelle fonction est marquée par la plus grande valeur initiale?
c) Quelles fonctions partagent la même valeur initiale?
d) Quelle parabole est ouverte vers le bas?
a)
Laquelle de ces fonctions s'associe à la parabole la plus ouverte? \(y_2\)
b)
Quelle fonction est marquée par la plus grande valeur initiale? \(y_3\)
c)
Quelles fonctions partagent la même valeur initiale? \(y_1\) et \(y_4\)
d)
Quelle parabole est ouverte vers le bas? \(y_4\)
La règle d'une fonction quadratique est f(x) = -3 ( x + 15)² + 25 sur le domaine x ε ] -∞, +∞[.
Laquelle des affirmations suivantes est vraie?
a) La fonction est croissante pour x ε ] -∞, 25]
b) La fonction est décroissante pour x ε [-15, +∞[
c) La fonction est positive pour x ε ] -∞, -15]
d) La fonction est positive pour x ε ] -∞, +∞[
b) La fonction est décroissante pour x ε [-15, +∞[
Formule une conjecture expliquant le lien entre la forme factorisée f(x)=a(x - x1)(x - x2)
d’une fonction polynomiale de degré 2 et son ordonnée à l’origine.
Suggestion: faire plusieurs exemples.
À la lumière de ces exemples, l'ordonnée à l'origine correspond au produit du paramètre a et des deux zéros.
Les fonctions polynomiales et la fonction quadratique de base.
La fonction quadratique transformée sous forme canonique.
La fonction quadratique transformée sous forme générale.
La fonction quadratique transformée sous forme factorisée.