Vidéo de théorie et exercices-Les paramètres d'une fonction
|
1- Écouter la vidéo ci-dessous. Si tu le préfères, tu peux écouter la vidéo par parties. Ces parties sont disponibles dans les onglets "Vidéo", après la série d'exercices. 2- Répondre aux exercices sur du papier. Les questions des exercices se retrouvent dans les onglets «Q» ci-dessous. 3- Corriger les exercices. Les réponses (corrigés) pour chacune des questions se retrouvent dans les onglets «R» ci-dessous. |
|
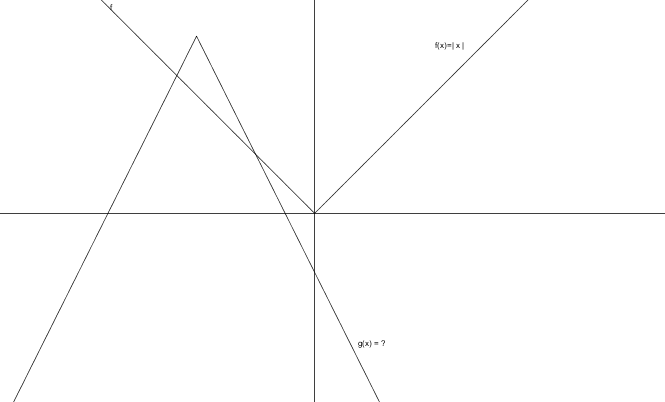
La fonction f(x) est la fonction de base de la valeur absolue. La fonction g(x) a été obtenue par transformation de f(x). Quelles sont les valeurs possibles des paramètres? Paramètre a : a > 0 ou a < 0 Paramètre h : h > 0 ou h < 0 Paramètre k : k > 0 ou k < 0 |
 |
a < 0, car il y a eu réflexion sur y=k(ouverture vers le bas)
h < 0, car il y a eu translation horizontale vers la gauche
k > 0, car il y a eu translation verticale vers le haut
Voici la représentation graphique de la fonction f(x) = √x.
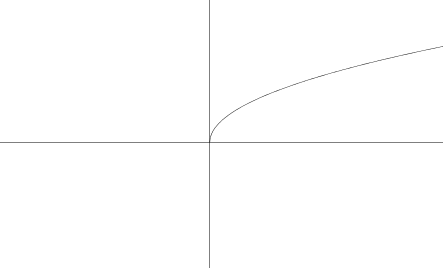
Quelle règle peut définir g(x) ci-dessous?
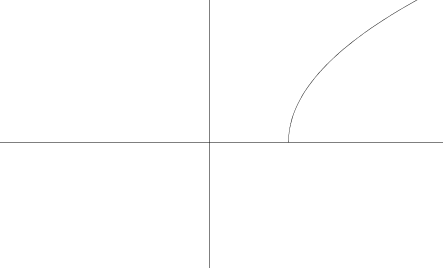
|
a) g(x)= b) g(x)= c) g(x)= d) g(x)= |
 |
La réponse est:
c) g(x)= 2√(x - 2)
h = 2, car il y a eu translation horizontale de 2 unités vers la droite
a= 2, changement d'échelle vertical de facteur 2 (a>1) et pas de réflexion (a>0).
Voici le graphique de f(x)= x², la fonction quadratique de base.
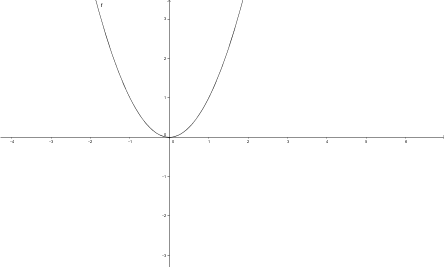
|
Déduis le graphique de: a) g(x)= (x - 3)² - 1 b) h(x)= -0,5x² + 2 c) i(x)= 2(x + 3)² |
 |
a)
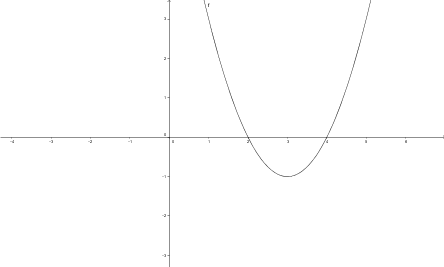
b)
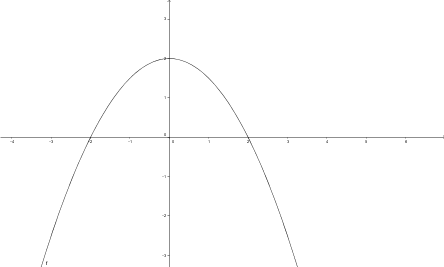
c)
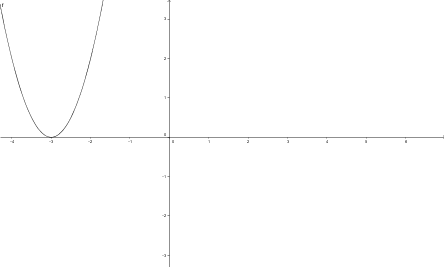
Détermine la règle de g(x) sachant que f(x) = [ x ].
Voici f(x):
Voici g(x):
g(x)= - [0,5(x - 1)]
a= -1 car la fonction est décroissante, les points pleins sont à gauche et la contremarche est de 1 unité.
b= 0,5 car la largeur des marches est de 2 unités alors b= ½
(h, k) = (1, 0) car point plein à (1, 0)
|
Soit les fonctions f et h représentées ci-dessus. La règle de f est f(x)= x² et celle de h est de la forme h(x)=ax². Dans quel intervalle se situe la valeur du paramètre a de la fonction h? a) ]-1, 0[ b) ]1, +∞[ c) ]-∞, -1[ d) ]0, 1[ |
 |
c) ]-∞, -1[
Car il y a eu un allongement vertical et une réflexion (ouverture vers le bas).
Introduction
Le paramètre a
Le paramètre b
Les paramètres h et k et exemples avec tous les paramètres à la fois.